题目内容
17.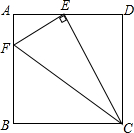 如图,已知E是矩形ABCD边AD的中点,F是AB上一点,EF⊥CE,若AB:BC=$\sqrt{3}$:2,同图中(有4个三角形)相似三角形有3对.
如图,已知E是矩形ABCD边AD的中点,F是AB上一点,EF⊥CE,若AB:BC=$\sqrt{3}$:2,同图中(有4个三角形)相似三角形有3对.
分析 由四边形ABCD是矩形,于是得到∠A=∠D=90°,根据CE⊥EF,得到∠AFE=∠DEC,即可得到结论.
解答  解:设AB=DC=$\sqrt{3}$x,BC=AD=2x,
解:设AB=DC=$\sqrt{3}$x,BC=AD=2x,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵CE⊥EF,
∴∠AFE+∠AEF=∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
∴△AEF∽△DCE.
此时$\frac{AE}{DC}$=$\frac{AF}{DE}$,即$\frac{x}{\sqrt{3}x}$=$\frac{AF}{x}$,
则AF=$\frac{\sqrt{3}}{3}$x
∴BF=$\frac{2\sqrt{3}}{3}$.
∴$\frac{AF}{BF}$=$\frac{AE}{BC}$=$\frac{1}{2}$.
又∵∠A=∠D,
∴△AEF∽△BCF.
∴△AEF∽△DCE∽△BCF.
故答案是:3.
点评 本题考查了相似三角形的性质,矩形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
8.一个不透明的布袋里装有9个只有颜色不同球,其中4个红球,5个白球,从布袋中随机摸出1个球,摸出的球是红球的概率为( )
| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{k^2}{x}$(x<0,k是不等于0的常数)图象上一点,AO的延长线交函数y=$\frac{1}{x}$(x>0)的图象于点C.点A关于y轴的对称点为A′;点C关于x轴的对称点为C′,关于原点对称点是C′′.连结CC′,交x轴于点B,连结AB,AA′,A′C′,若△ABC的面积等于2,则四边形A A′C′C′′的面积等于( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{k^2}{x}$(x<0,k是不等于0的常数)图象上一点,AO的延长线交函数y=$\frac{1}{x}$(x>0)的图象于点C.点A关于y轴的对称点为A′;点C关于x轴的对称点为C′,关于原点对称点是C′′.连结CC′,交x轴于点B,连结AB,AA′,A′C′,若△ABC的面积等于2,则四边形A A′C′C′′的面积等于( ) 如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍.
如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍. 如图所示,把一个等腰三角形纸片按底边上的高线剪开成为两个三角形纸片,现在要用这两个三角形纸片拼合成与原等腰三角形不同的三角形或四边形,并且要求拼合成的图形是轴对称图形,则这样的图形有3个.
如图所示,把一个等腰三角形纸片按底边上的高线剪开成为两个三角形纸片,现在要用这两个三角形纸片拼合成与原等腰三角形不同的三角形或四边形,并且要求拼合成的图形是轴对称图形,则这样的图形有3个.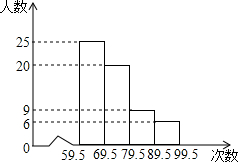 如图是九年级(1)班同学的一次体检每分钟心跳次数的频数分布直方图(次数均为整数).已知该班只有5位同学的心跳每分钟75次.请观察图回答:
如图是九年级(1)班同学的一次体检每分钟心跳次数的频数分布直方图(次数均为整数).已知该班只有5位同学的心跳每分钟75次.请观察图回答: