题目内容
2.已知反比例函数的图象过点(2,-1).(1)求这个函数的关系式,并画出图象.
(2)若点A(-5,m)在其图象上,则点A关于两坐标轴和原点的对称点是否还在图象上?
分析 (1)直接将A点代入函数解析式求出答案,再画出图象;
(2)首先利用关于关于两坐标轴和原点的对称点得出各对应点坐标,进而判断即可.
解答 解:(1)设反比例函数解析式为:y=$\frac{k}{x}$,
则k=2×(-1)=-2,
故反比例函数解析式为:y=-$\frac{2}{x}$,
如图所示: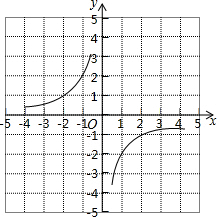 ;
;
(2)∵点A(-5,m)在其图象上,
∴m=-$\frac{2}{-5}$=$\frac{2}{5}$,
∴A(-5,$\frac{2}{5}$),
∴点A关于x坐标轴对称点的坐标为:(-5,-$\frac{2}{5}$),
点A关于y坐标轴对称点的坐标为:(5,$\frac{2}{5}$),
点A关于原点的对称点的坐标为:(5,-$\frac{2}{5}$),
∵-5×(-$\frac{2}{5}$)=2≠-2,
∴点A关于x坐标轴对称点不在图象上;
∵5×$\frac{2}{5}$=2≠-2,
∴点A关于y坐标轴对称点不在图象上;
∵5×(-$\frac{2}{5}$)=-2=-2,
∴点A关于原点对称点在图象上.
点评 此题主要考查了待定系数法求反比例函数解析式以及关于坐标轴对称点的性质,正确得出A点坐标是解题关键.

练习册系列答案
相关题目
18.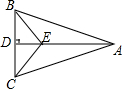 如图,AD⊥BC,垂足为D,BD=DC,则图中全等的三角形共有( )
如图,AD⊥BC,垂足为D,BD=DC,则图中全等的三角形共有( )
 如图,AD⊥BC,垂足为D,BD=DC,则图中全等的三角形共有( )
如图,AD⊥BC,垂足为D,BD=DC,则图中全等的三角形共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
 由6个完全相同的小正方体搭成的几何体如图所示,它的俯视图是( )
由6个完全相同的小正方体搭成的几何体如图所示,它的俯视图是( )



 如图,D是BC上一点,AB=AD,BC=DE,AC=AE,试说明:△ABC≌△ADE.
如图,D是BC上一点,AB=AD,BC=DE,AC=AE,试说明:△ABC≌△ADE.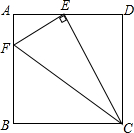 如图,已知E是矩形ABCD边AD的中点,F是AB上一点,EF⊥CE,若AB:BC=$\sqrt{3}$:2,同图中(有4个三角形)相似三角形有3对.
如图,已知E是矩形ABCD边AD的中点,F是AB上一点,EF⊥CE,若AB:BC=$\sqrt{3}$:2,同图中(有4个三角形)相似三角形有3对.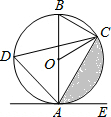 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠CAE=∠ADC.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠CAE=∠ADC.