题目内容
16.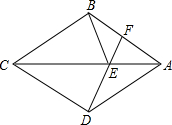 如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE.
如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE.
分析 根据菱形的性质得出∠BCE=∠DCE,BC=CD,AB∥CD,推出∠AFD=∠CDE,证△BCE≌△DCE,推出∠CBE=∠CDE即可.
解答 证明:∵四边形ABCD是菱形,
∴∠BCE=∠DCE,BC=CD,AB∥CD,
∴∠AFD=∠CDE,
在△BCE和△DCE中
$\left\{\begin{array}{l}{BC=CD}\\{∠BCE=∠DCE}\\{CE=CE}\end{array}\right.$,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,
∵∠AFD=∠CDE,
∴∠AFD=∠CBE.
点评 此题主要考查了菱形的判定与性质以及全等三角形的判定与性质等知识,得出△BCE≌△DCE是解题关键.

练习册系列答案
相关题目
7.在△ABC中,∠A=62°,点I是外接圆圆心,则∠BIC=124度.
在△ABC中,O是△ABC的内心,若∠A=50°,则∠BOC=115°.
一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
在△ABC中,O是△ABC的内心,若∠A=50°,则∠BOC=115°.
一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
6.已知a,b,c是△ABC的三条边的边长,且p=$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$,则( )
| A. | 存在三角形使得p=1或p=2 | B. | 0<p<1 | ||
| C. | 1<p<2 | D. | 2<p<3 |
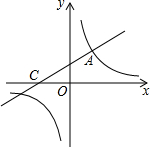 如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(m,3),与x轴交于点C.