题目内容
5.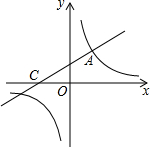 如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(m,3),与x轴交于点C.(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
分析 (1)把A坐标代入直线解析式求出m的值,确定出A坐标,即可确定出双曲线解析式;
(2)设P(x,0),表示出PC的长,高为A纵坐标,根据三角形ACP面积求出x的值,确定出P坐标即可.
解答 解:(1)把A(m,3)代入直线解析式得:3=$\frac{1}{2}$m+2,即m=2,
∴A(2,3),
把A坐标代入y=$\frac{k}{x}$,得k=6,
则双曲线解析式为y=$\frac{6}{x}$;
(2)对于直线y=$\frac{1}{2}$x+2,令y=0,得到x=-4,即C(-4,0),
设P(x,0),可得PC=|x+4|,
∵△ACP面积为3,
∴$\frac{1}{2}$|x+4|•3=3,即|x+4|=2,
解得:x=-2或x=-6,
则P坐标为(-2,0)或(-6,0).
点评 此题考查了反比例函数与一次函数的交点问题,涉及的知识有:待定系数法确定函数解析式,坐标与图形性质,以及三角形面积求法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
15.在平行投影下,线段AB在投影面上的投影为线段A'B',则( )
| A. | AB=A'B' | B. | AB≥A'B' | C. | AB<A'B' | D. | 以上都有可能 |
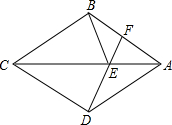 如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE.
如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE. 如图,把一张矩形纸片ABCD沿对角线DB折叠,DE交AB于F,连AE.若∠DBC=58°,则∠AEF=32°.
如图,把一张矩形纸片ABCD沿对角线DB折叠,DE交AB于F,连AE.若∠DBC=58°,则∠AEF=32°. 如图所示,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图所示,∠A+∠B+∠C+∠D+∠E+∠F=360°.
 如图,在直角坐标系中,点A,点B的坐标分别为(2,0),(0,2)
如图,在直角坐标系中,点A,点B的坐标分别为(2,0),(0,2)