题目内容
12.已知关于x的一元二次方程x2-(2k+1)x+k2+k=0(k≠0)有两个实数根.(1)判断该方程的两个实数根是否相等,并说明理由;
(2)已知k=9,若△ABC的两边的长分别是这个方程的两个实数根,第三边的长为6,求△ABC的周长.
分析 (1)先计算出△=1,然后根据判别式的意义即可得出该方程的两个实数根不相等;
(2)将k=9代入x2-(2k+1)x+k2+k=0,得出方程为x2-19x+90=0,由根与系数的关系得出两根之和为19,那么△ABC的周长=19+6=25.
解答 解:(1)该方程的两个实数根不相等,理由如下:
∵△=(2k+1)2-4(k2+k)=1>0,
∴方程有两个不相等的实数根,即该方程的两个实数根不相等;
(2)k=9时,方程为x2-19x+90=0,
由根与系数的关系可得,两根之和为19,
∵△ABC的两边的长分别是这个方程的两个实数根,第三边的长为6,
∴△ABC的周长=19+6=25.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了根与系数的关系.

练习册系列答案
相关题目
4.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三边之比为3:4:5 | B. | 三边长为1,$\sqrt{3}$,2 | ||
| C. | 三边长为$\sqrt{11}$,2,4 | D. | 三边长a,b,c满足a2=(c+b)(c-b) |
 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长为7m.
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长为7m.
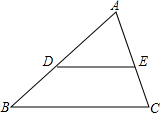 如图所示,在△ABC中,点D、E分别在AB,AC上,已知∠B=∠ADE,推理填空:
如图所示,在△ABC中,点D、E分别在AB,AC上,已知∠B=∠ADE,推理填空: