题目内容
4.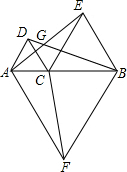 已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,以AB为边向AD所在的另一侧作等边△ABF,AE、B0相交于G,连结CF.求证:AE=BD=CF.
已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,以AB为边向AD所在的另一侧作等边△ABF,AE、B0相交于G,连结CF.求证:AE=BD=CF.
分析 分别证明△DAB≌△CAF和△ACE≌△DCB,则BD=CF,AE=BD,可证得AE=BD=CF.
解答 证明:∵△ADC、△BCE、△ABF都是等边三角形,
∴AD=AC=DC,AB=AF,CE=BC,∠DAB=∠CAF=60°,∠ACE=∠DCB=120°,
在△DAB和△CAF中,
$\left\{\begin{array}{l}{AD=AC}\\{∠DAB=∠CAF}\\{AB=AF}\end{array}\right.$,
∴△DAB≌△CAF(SAS),
∴BD=CF,
在△ACE和△DCB中,
$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{CE=BC}\end{array}\right.$,
∴△ACE≌△DCB(SAS),
∴AE=BD,
∴AE=BD=CF.
点评 本题主要考查了全等三角形的判定与性质以及等边三角形的性质,熟练掌握全等三角形的判定方法以及等边三角形的性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.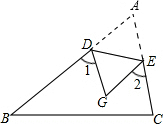 如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
 如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )| A. | 50° | B. | 65° | C. | 100° | D. | 130° |
12.如果两个相似三角形的面积比是1:9,那么它们的周长比是( )
| A. | 1:9 | B. | 1:3 | C. | 1:4.5 | D. | 1:8 |
13.下列各式中变形正确的是( )
| A. | $\frac{\frac{1}{3}x+\frac{1}{4}y}{\frac{3}{4}x-\frac{1}{6}y}$=$\frac{4x+3y}{10x+3y}$ | B. | $\frac{\frac{1}{3}x-\frac{1}{4}y}{\frac{5}{4}x+\frac{1}{6}y}$=$\frac{4x-3y}{10x+3y}$ | ||
| C. | $\frac{\frac{2}{3}x-\frac{3}{4}y}{\frac{3}{4}x-\frac{1}{6}y}$=$\frac{8x-9y}{9x-2y}$ | D. | $\frac{\frac{1}{3}x+\frac{1}{4}y}{\frac{5}{4}x-\frac{1}{6}y}$=$\frac{4x+3y}{10x-3y}$ |
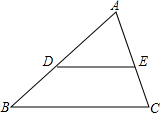 如图所示,在△ABC中,点D、E分别在AB,AC上,已知∠B=∠ADE,推理填空:
如图所示,在△ABC中,点D、E分别在AB,AC上,已知∠B=∠ADE,推理填空: 二次函数y=ax2+bx+c的图象如图所示,不求函数解析式,根据图象解答下列问题:
二次函数y=ax2+bx+c的图象如图所示,不求函数解析式,根据图象解答下列问题: