题目内容
已知x满足x2-3x-1=0.求x4-
的值.
| 1 |
| x4 |
考点:分式的混合运算,完全平方公式
专题:计算题
分析:已知等式两边除以x,求出x-
的值,两边平方求出x2+
的值,进而求出x+
的值,原式利用平方差公式化简,将各自的值代入计算即可求出值.
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
解答:
解:x2-3x-1=0,
两边除以x得:x-
=3,
两边平方得:(x-
)2=x2+
-2=9,即x2+
=11,
∴(x+
)2=x2+
+2=11+2=13,即x+
=±
,
∴x2-
=(x+
)(x-
)=±3
,
则原式=(x2-
)(x2+
)=±33
.
两边除以x得:x-
| 1 |
| x |
两边平方得:(x-
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x2 |
∴(x+
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 13 |
∴x2-
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 13 |
则原式=(x2-
| 1 |
| x2 |
| 1 |
| x2 |
| 13 |
点评:此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
将一个两位数的个位数字与十位数字相互交换位置,得到另一个两位数,则这个新两位数与原来两位数的差,一定可以被( )
| A、2整除 | B、3整除 |
| C、6整除 | D、11整除 |
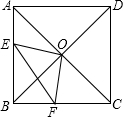 正方形ABCD中,AC,BD交于O,∠EOF=90°,已知AE=3,CF=4.则S△BEF为
正方形ABCD中,AC,BD交于O,∠EOF=90°,已知AE=3,CF=4.则S△BEF为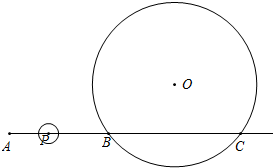 已知点C在射线AB上(点B在A、C之间),AB=12cm,BC=16cm,有一半径为10cm的⊙O过B、C两点,点P为射线AB上的一动点,且从点A出发,以1cm/秒的速度沿射线AB方向运动,设运动时间为t秒(t≥0),若以1cm为半径的⊙P与⊙O没有公共点,则t的取值范围为
已知点C在射线AB上(点B在A、C之间),AB=12cm,BC=16cm,有一半径为10cm的⊙O过B、C两点,点P为射线AB上的一动点,且从点A出发,以1cm/秒的速度沿射线AB方向运动,设运动时间为t秒(t≥0),若以1cm为半径的⊙P与⊙O没有公共点,则t的取值范围为 如图,直线y=ax+b经过点(0,1)和(2,0),则不等式ax+b<-1的解集为
如图,直线y=ax+b经过点(0,1)和(2,0),则不等式ax+b<-1的解集为