题目内容
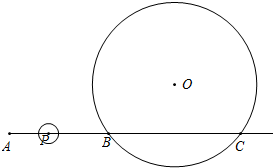已知点C在射线AB上（点B在A、C之间），AB=12cm，BC=16cm，有一半径为10cm的⊙O过B、C两点，点P为射线AB上的一动点，且从点A出发，以1cm/秒的速度沿射线AB方向运动，设运动时间为t秒（t≥0），若以1cm为半径的⊙P与⊙O没有公共点，则t的取值范围为考点：圆与圆的位置关系
专题：动点型
分析：首先过点O作OE⊥BC于点E，连接OP，OB，然后分别求得⊙P与⊙O外切与内切时PE的长，继而求得答案．
解答：
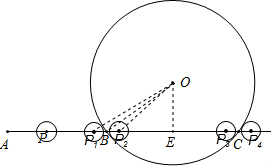解：过点O作OE⊥BC于点E，连接OP，OB，
∴BE=
BF=
×16=8，
∴OE=
=
=6，
当⊙P与⊙O外切时，OP=10+1=11，
∴EP=
=
，
∴AP1=AB+BE-EP=12+8-
=20-
，AP4=AE+EP=20+
，
当⊙P与⊙O内切时，OP=10-1=9，
∴EP=
=3
，
∴AP2=AE-PE=20-3
，AP3=AE+EP=20+3
，
∴⊙P与⊙O没有公共点，则t的取值范围为：0≤t＜20-
或20-3
＜t＜20+3
或t＞20+
．
故答案为：0≤t＜20-
或20-3
＜t＜20+3
或t＞20+
．
解：过点O作OE⊥BC于点E，连接OP，OB，∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=
| OB2-BE2 |
| 102-82 |
当⊙P与⊙O外切时，OP=10+1=11，
∴EP=
| OP2-OE2 |
| 85 |
∴AP1=AB+BE-EP=12+8-
| 85 |
| 85 |
| 85 |
当⊙P与⊙O内切时，OP=10-1=9，
∴EP=
| OP2-OE2 |
| 5 |
∴AP2=AE-PE=20-3
| 5 |
| 5 |
∴⊙P与⊙O没有公共点，则t的取值范围为：0≤t＜20-
| 85 |
| 5 |
| 5 |
| 85 |
故答案为：0≤t＜20-
| 85 |
| 5 |
| 5 |
| 85 |
点评：此题考查了圆与圆的位置关系．此题比较适中，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系．
练习册系列答案
优学名师名题系列答案
相关题目
二元一次方程组
的解是（ ）
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如图，是一个转盘，转盘被分成两个扇形，颜色分为白黑黄两种，黑色扇形的圆心角为150°，指针固定，转动转盘后任其自由停止，某个扇形会停在指针所指的位置，（指针指向交线时当作指向右边的扇形）则指针指向黑色扇形的概率是下列各组数中，相等的是（ ）
| A、（-1）3和1 | ||
| B、（-1）2和-1 | ||
| C、-（-1）和|-1| | ||
D、
|