Question

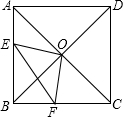正方形ABCD中，AC，BD交于O，∠EOF=90°，已知AE=3，CF=4．则S_△BEF为

 

．

Answer 1

考点：全等三角形的判定与性质,正方形的性质

专题：

分析：结合正方形的性质可证到△AOE≌△BOF，则有AE=BF=3，即可得到AB=BC=7，从而可求出EB=4，由此可求出△BEF的面积．

解答： 解：∵四边形ABCD是正方形，
∴AB=BC，OA=OB，∠ABC=∠AOB=90°，∠BAC=∠CBD=45°．
∵∠EOF=90°，
∴∠AOE=∠BOF=90°-∠EOB．
在△AOE和△BOF中，

∠AOE=∠BOF OA=OB ∠EAO=∠FBO

，
∴△AOE≌△BOF（ASA），
∴AE=BF=3，
∴BC=BF+FC=3+4=7，
∴AB=BC=7，
∴BE=AB-AE=7-3=4，
∴S_△BEF=

1

2

BE•BF=

1

2

×4×3=6．
故答案为6．

点评：本题主要考查了正方形的性质、全等三角形的判定与性质等知识，证到△AOE≌△BOF是解决本题的关键．