题目内容
10.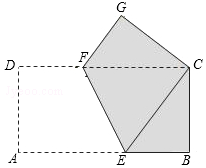 矩形纸片ABCD的边长AB=8,AD=4,将矩形纸片沿EF折叠,使点A与点C重合,折叠后在某一面着色(如图),则着色部分的面积为22.
矩形纸片ABCD的边长AB=8,AD=4,将矩形纸片沿EF折叠,使点A与点C重合,折叠后在某一面着色(如图),则着色部分的面积为22.
分析 根据折叠的性质得到CG=AD=4,GF=DF=CD-CF,∠G=90°,根据勾股定理求出FC,根据三角形的面积公式计算即可.
解答 解:由折叠的性质可得:CG=AD=4,GF=DF=CD-CF,∠G=90°,
则△CFG为直角三角形,
在Rt△CFG中,FC2=CG2+FG2,即FC2=42+(8-FC)2,
解得:FC=5,
∴△CEF的面积=$\frac{1}{2}$×FC×BC=10,
△BCE的面积=△CGF的面积=$\frac{1}{2}$×FG×GC=6,
则着色部分的面积为:10+6+6=22,
故答案为:22.
点评 本题考查的是翻转变换的性质、勾股定理的应用,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 正五角星 | D. | 正六边形 |
15.若关于x的方程$\frac{x}{x-2}$-$\frac{m}{{{x^2}-4}}$=1的解为正数,则m的取值范围是( )
| A. | m<4 | B. | m>4 | C. | m<4且m≠0 | D. | m>4且m≠8 |
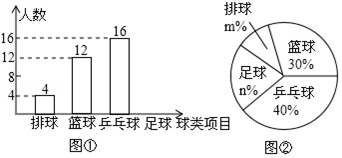
 某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量x(GB)的之间的函数关系.
某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量x(GB)的之间的函数关系. 如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则$\frac{EF}{GH}$的值为$\sqrt{3}$.
如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则$\frac{EF}{GH}$的值为$\sqrt{3}$. 如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移$\sqrt{2}$个单位,则平移后直线的解析式为y=2x.
如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移$\sqrt{2}$个单位,则平移后直线的解析式为y=2x.