题目内容
15.若关于x的方程$\frac{x}{x-2}$-$\frac{m}{{{x^2}-4}}$=1的解为正数,则m的取值范围是( )| A. | m<4 | B. | m>4 | C. | m<4且m≠0 | D. | m>4且m≠8 |
分析 先将方程进行求解,然后利用x>0列出方程即可求出m的范围.
解答 解:去分母可得:x2+2x-m=x2-4
∴x=$\frac{m-4}{2}$
∵x>0,
∴$\frac{m-4}{2}$>0,
∴m>4
又∵x2-4≠0,
∴x≠±2,
∴m≠0或8,
∴m的范围为:m>4且m≠8,
故选(D)
点评 本题考查分式方程的解,解题的关键是求出x的表达式以及限制条件,本题属于中等题型.

练习册系列答案
相关题目
 如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=$\frac{1}{3}$;若S△ABC=12,则S△ADF-S△BEF=2.
如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=$\frac{1}{3}$;若S△ABC=12,则S△ADF-S△BEF=2.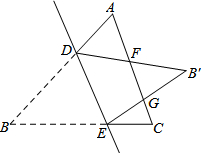 如图,已知△ABC中,AC=BC,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在B'处,DB'、EB'分别交AC于点F、G,若∠ADF=66°,则∠EGC的度数为66°.
如图,已知△ABC中,AC=BC,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在B'处,DB'、EB'分别交AC于点F、G,若∠ADF=66°,则∠EGC的度数为66°.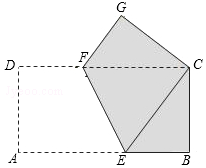 矩形纸片ABCD的边长AB=8,AD=4,将矩形纸片沿EF折叠,使点A与点C重合,折叠后在某一面着色(如图),则着色部分的面积为22.
矩形纸片ABCD的边长AB=8,AD=4,将矩形纸片沿EF折叠,使点A与点C重合,折叠后在某一面着色(如图),则着色部分的面积为22. 请在如图所示的方格内(每个小表格的边长均为1)画出△ABC,使它的顶点都在格点上,且AC=2,AB=2$\sqrt{5}$,BC=2$\sqrt{2}$,求:
请在如图所示的方格内(每个小表格的边长均为1)画出△ABC,使它的顶点都在格点上,且AC=2,AB=2$\sqrt{5}$,BC=2$\sqrt{2}$,求: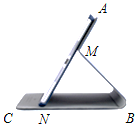 如图为一种平板电脑保护套的支架侧视图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架,为了观看舒适,可以调整倾斜角∠ANB的大小,但平板的下端点N只能在底座边CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图(见答题纸),其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN,根据以上数据,判断倾斜角∠ANB能小于30°吗?请说明理由.
如图为一种平板电脑保护套的支架侧视图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架,为了观看舒适,可以调整倾斜角∠ANB的大小,但平板的下端点N只能在底座边CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图(见答题纸),其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN,根据以上数据,判断倾斜角∠ANB能小于30°吗?请说明理由.