题目内容
1.阅读材料,回答问题:化简$\frac{1}{\sqrt{2}+1}$:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}+1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\frac{\sqrt{2}-1}{(\sqrt{2})^{2}-1}$=$\sqrt{2}$-1;
化简:$\frac{2}{3-\sqrt{5}}$:$\frac{2}{3-\sqrt{5}}$=$\frac{2(3+\sqrt{5})}{(3-\sqrt{5})(3+\sqrt{5})}$=$\frac{2(3+\sqrt{5})}{{3}^{2}-(\sqrt{5})^{2}}$=$\frac{2(3+\sqrt{5})}{4}$=$\frac{3+\sqrt{5}}{2}$.
(1)以上化简过程运用了哪个乘法公式?
(2)依照上述化简方法化简$\frac{2}{\sqrt{5}+\sqrt{3}}$;
(3)计算:$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$的值.
分析 (1)根据平方差公式即可求解;
(2)分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式,依此即可求解;
(3)先分母有理化,再抵消法求解即可.
解答 解:(1)化简过程运用了平方差公式;
(2)$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\frac{2×(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5})^{2}-(\sqrt{3})^{2}}$=$\frac{2(\sqrt{5}-\sqrt{3})}{2}$=$\sqrt{5}$-$\sqrt{3}$;
(3)$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$+…+10-3$\sqrt{11}$
=10-1
=9.
点评 考查了分母有理化,关键是熟悉分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.2016年4月14日,永远的科比狂砍60分完美谢幕,打破NBA球员退役战得分纪录,成为NBA历史单场60+年纪最大的球员,其中罚球12罚10中,命中率大约是83.3%,下列说法错误的是( )
| A. | 科比罚球投篮12次,不一定全部命中 | |
| B. | 科比罚球投篮120次,一定命中100次 | |
| C. | 科比罚球投篮1次,命中的可能性较大 | |
| D. | 科比罚球投篮1次,不命中的可能性较小 |
6.(x2+mx+1)(x-3)的积中x的二次项系数为零,则m的值是( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
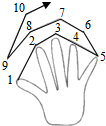 如图,我们做一个游戏:从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→食指…的顺序依次数正整数1、2、3、4、5…,当第(n+1)次数到中指时,恰好数到的数是3+4n(用含n的代数式表示).
如图,我们做一个游戏:从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→食指…的顺序依次数正整数1、2、3、4、5…,当第(n+1)次数到中指时,恰好数到的数是3+4n(用含n的代数式表示).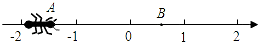 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则(m-1)(m-3)的值为1.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则(m-1)(m-3)的值为1.