题目内容
20.小明与小红邻准备为某个展览会做志愿者,展览会的举办时间为6月1日至6月5日这5天,小明随机选择连续2天,小红随机选择连续3天做志愿者.(1)小明选择6月2日、6月3日这两天的概率是多少?
(2)若小明、小红能在同一天做志愿者,他们就能合作,求他们能合作2天的概率.
分析 (1)根据题意列出随机选择连续2天的所有结果,找到符合条件的结果,利用概率公式计算即可;
(2)可通过列表或画树状图枚举所有等可能结果,在所有结果中找到使他们能合作2天的结果数,利用概率公式计算即可.
解答 解:(1)小明在6月1日至6月5日这5天中随机选择连续2天,有:1、2,2、3,3、4,4、5这4种等可能结果,
其中小明选择6月2日、6月3日这两天的结果仅有1种,
∴小明选择6月2日、6月3日这两天的概率是$\frac{1}{4}$;
(2)列表如下:
| 1、2 | 2、3 | 3、4 | 4、5 | |
| 1、2、3 | 1、2,1、2、3 | 2、3,1、2、3 | 3、4,1、2、3 | 4、5,1、2、3 |
| 2、3、4 | 1、2,2、3、4 | 2、3,2、3、4 | 3、4,2、3、4 | 4、5,2、3、4 |
| 3、4、5 | 1、2,3、4、5 | 2、3,3、4、5 | 3、4,3、4、5 | 4、5,3、4、5 |
∴他们能合作2天的概率为$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查列表法或画树状图法求概率,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
15. 正方形网格中,∠AOB如图放置,则∠AOB的正弦值为( )
正方形网格中,∠AOB如图放置,则∠AOB的正弦值为( )
 正方形网格中,∠AOB如图放置,则∠AOB的正弦值为( )
正方形网格中,∠AOB如图放置,则∠AOB的正弦值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
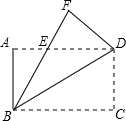 如图,把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E.
如图,把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E. 解不等式组$\left\{\begin{array}{l}{3x+1≥-5①}\\{2x-1≤3②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{3x+1≥-5①}\\{2x-1≤3②}\end{array}\right.$ 如图,点A是反比例函数图象上y=$\frac{k}{x}$一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则k=-3.
如图,点A是反比例函数图象上y=$\frac{k}{x}$一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则k=-3. 如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2=72°.
如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2=72°.