题目内容
15. 正方形网格中,∠AOB如图放置,则∠AOB的正弦值为( )
正方形网格中,∠AOB如图放置,则∠AOB的正弦值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 找出以∠AOB为内角的直角三角形,根据正弦函数的定义,即直角三角形中∠AOB的对边与斜边的比,就可以求出.
解答 解:如图,作EF⊥OB,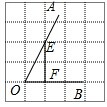
则EF=2,OF=1,由勾股定理得,OE=$\sqrt{5}$,
∴sin∠AOB=$\frac{EF}{OE}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
故选:B.
点评 本题考查的是锐角三角函数的定义及勾股定理,熟知正方形网格的特点,能在∠AOB的边上找出两点使△EOF恰好构成直角三角形是解答此题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图,在矩形ABCD中,点E、F分别在边BC、AD上,连结DE、EF.四边形CDFE沿EF折叠后得到四边形C′D′FE,点D的对称点D′与点B重合.求证:四边形BEDF是菱形.
如图,在矩形ABCD中,点E、F分别在边BC、AD上,连结DE、EF.四边形CDFE沿EF折叠后得到四边形C′D′FE,点D的对称点D′与点B重合.求证:四边形BEDF是菱形. 下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2016个梅花图案中,共有504个“
下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2016个梅花图案中,共有504个“ ”图案.
”图案.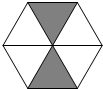 如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在黑色三角形区域的概率为$\frac{1}{3}$.
如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在黑色三角形区域的概率为$\frac{1}{3}$.