题目内容
12.竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=1.6.分析 设各自抛出后1.1秒时到达相同的最大离地高度为h,这个最大高度为h,则小球的高度y=a(t-1.1)2+h,根据题意列出方程即可解决问题.
解答 解:方法一:设各自抛出后1.1秒时到达相同的最大离地高度为h,这个最大高度为h,则小球的高度y=a(t-1.1)2+h,
由题意a(t-1.1)2+h=a(t-1-1.1)2+h,
解得t=1.6.
故第一个小球抛出后1.6秒时在空中与第二个小球的离地高度相同.
方法二:结合函数图象可知,两个抛物线的对称轴分别为x=1.1,x=2.1,
t在两条对称轴的中间,故t=$\frac{1}{2}$(1.1+2.1)=1.6
故答案为1.6.
点评 本题考查二次函数的应用,解题的关键是构建二次函数,学会把问题转化为我们学过的知识,利用方程的思想解决问题,属于中考常考题型.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 北京市2010-2015年机动车保有量统计如图所示.根据统计图中提供的信息,预估2016年北京市机动车的保有量约562万辆,你的预估理由是从各年的保有量增长看,汽车已趋于饱和,故2016年保有量相对2015年变化不大.
北京市2010-2015年机动车保有量统计如图所示.根据统计图中提供的信息,预估2016年北京市机动车的保有量约562万辆,你的预估理由是从各年的保有量增长看,汽车已趋于饱和,故2016年保有量相对2015年变化不大. 下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2016个梅花图案中,共有504个“
下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2016个梅花图案中,共有504个“ ”图案.
”图案.
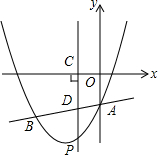 如图,抛物线y=x2+bx+c与直线y=$\frac{1}{2}$x-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
如图,抛物线y=x2+bx+c与直线y=$\frac{1}{2}$x-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.