题目内容
5. 如图,点A是反比例函数图象上y=$\frac{k}{x}$一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则k=-3.
如图,点A是反比例函数图象上y=$\frac{k}{x}$一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则k=-3.
分析 设点A的坐标为(m,n),先证明四边形ABCD为平行四边形,再根据平行四边形的面积公式结合点A的坐标,即可得出k的值.
解答 解:设点A的坐标为(m,n),
∵AB⊥y轴,CD⊥y轴,
∴AB∥CD,
又∵BC∥AD,
∴四边形ABCD为平行四边形.
S平行四边形ABCD=AB•OB=-m•n=3,
∴k=mn=-3.
故答案为:-3.
点评 本题考查了反比例函数图象上点的坐标特征、平行四边形的判定定理以及平行四边形的面积公式,解题的关键是求出点A的横纵坐标之积.本题属于基础题,难度不大,解决该题型题目时,用点A的坐标来表示平行四边形的面积是关键.

练习册系列答案
相关题目
15.已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
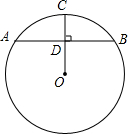 如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16.
如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16. 如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=82°,则∠B=49°.
如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=82°,则∠B=49°.
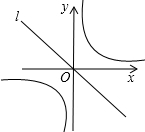 如图,已知直线l:y=-x,双曲线y=$\frac{1}{x}$,在l上取一点A(a,-a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为$\sqrt{2}$或$\frac{\sqrt{2}}{2}$.
如图,已知直线l:y=-x,双曲线y=$\frac{1}{x}$,在l上取一点A(a,-a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为$\sqrt{2}$或$\frac{\sqrt{2}}{2}$.