题目内容
10.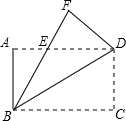 如图,把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E.
如图,把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E.(1)求证:△BEA≌△DEF;
(2)若AB=2,AD=4,求AE的长.
分析 (1)根据矩形的性质得出AB=CD,∠A=∠C=90°,根据折叠得出DF=CD,∠F=∠C=90°,求出AB=FD,∠A=∠F,根据全等三角形的判定得出即可;
(2)根据全等得出BE=DE,根据勾股定理得出关于AE的方程,求出方程的解即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,
∵把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E,
∴DF=CD,∠F=∠C=90°,
∴AB=FD,∠A=∠F,
在△BEA和△DEF中
$\left\{\begin{array}{l}{∠AEB=∠FED}\\{∠A=∠F}\\{AB=DF}\end{array}\right.$
∴△BEA≌△DEF(AAS);
(2)解:∵△BEA≌△DEF,
∴BE=DE=AD-AE=4-AE,
在Rt△BAE中,由勾股定理得:AB2+AE2=BE2,
∴22+AE2=(4-AE)2,
解得:AE=$\frac{3}{2}$.
点评 本题考查了勾股定理,折叠的性质,矩形的性质的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
20.如图,三个图形是由立体图形展开得到的,相应的立体图形顺序是( )


| A. | 圆柱、三棱柱、圆锥 | B. | 圆锥、三棱柱、圆柱 | ||
| C. | 圆柱、三棱锥、圆锥 | D. | 圆柱、三棱柱、半球 |

 如图,?ABCD的对角线AC,BD相交于点O,点E是边AD的中点,若△BCD的周长为18,则△DEO的周长是9.
如图,?ABCD的对角线AC,BD相交于点O,点E是边AD的中点,若△BCD的周长为18,则△DEO的周长是9.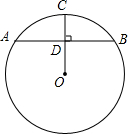 如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16.
如图,在⊙O中,AB为⊙O的弦,半径OC⊥AB于点D,若OB的长为10,sin∠BOD=$\frac{4}{5}$,则AB的长为16. 北京市2010-2015年机动车保有量统计如图所示.根据统计图中提供的信息,预估2016年北京市机动车的保有量约562万辆,你的预估理由是从各年的保有量增长看,汽车已趋于饱和,故2016年保有量相对2015年变化不大.
北京市2010-2015年机动车保有量统计如图所示.根据统计图中提供的信息,预估2016年北京市机动车的保有量约562万辆,你的预估理由是从各年的保有量增长看,汽车已趋于饱和,故2016年保有量相对2015年变化不大.