题目内容
19.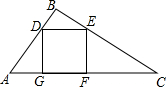 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )| A. | $\frac{6}{7}$ | B. | $\frac{30}{37}$ | C. | $\frac{12}{7}$ | D. | $\frac{60}{37}$ |
分析 过点B作BP⊥AC,垂足为P,BP交DE于Q,三角形的面积公式求出BP的长度,由相似三角形的判定定理得出△BDE∽△BAC,设边长DE=x,根据相似三角形的对应边成比例求出x的长度可得.
解答 解:如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.
∵S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•BP,
∴BP=$\frac{AB•BC}{AC}$=$\frac{3×4}{5}$=$\frac{12}{5}$.
∵DE∥AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴$\frac{DE}{AC}=\frac{BQ}{BP}$.
设DE=x,则有:$\frac{x}{5}=\frac{\frac{12}{5}-x}{\frac{12}{5}}$,
解得x=$\frac{60}{37}$,
故选:D.
点评 本题主要考查把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程即可求出边长,熟练掌握对应高的比等于相似比是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目