题目内容
9.已知圆的半径是2$\sqrt{3}$,则该圆的内接正六边形的面积是18$\sqrt{3}$.分析 根据正六边形被它的半径分成六个全等的等边三角形,再根据等边三角形的边长,求出等边三角形的高,再根据面积公式即可得出答案.
解答 解:连接正六边形的中心与各个顶点,得到六个等边三角形,
∵等边三角形的边长是2$\sqrt{3}$,
∴高为3,
∴等边三角形的面积是3$\sqrt{3}$,
∴正六边形的面积是:18$\sqrt{3}$;
故答案为:18$\sqrt{3}$.
点评 本题考查了正多边形和圆,解题的关键要记住正六边形的特点,它被半径分成六个全等的等边三角形.

练习册系列答案
相关题目
17.点B(0,-3)在( )
| A. | x轴的正半轴上 | B. | x轴的负半轴上 | C. | y轴的正半轴上 | D. | y轴的负半轴上 |
14.若|x|=5,|y|=3,则|x-y|等于( )
| A. | 2 | B. | ±8 | C. | 8或2 | D. | ±8或±2 |
19.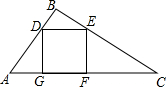 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )| A. | $\frac{6}{7}$ | B. | $\frac{30}{37}$ | C. | $\frac{12}{7}$ | D. | $\frac{60}{37}$ |
 如图,在边长为6$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
如图,在边长为6$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论: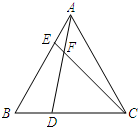 如图,在等边△ABC中,点D,E分别在边BC,AB上,AD与CE交于点F,CE=AD,∠DFC=60度.求证:BD=AE.
如图,在等边△ABC中,点D,E分别在边BC,AB上,AD与CE交于点F,CE=AD,∠DFC=60度.求证:BD=AE. 如图,已知一次函数y=-$\frac{1}{2}$x+2的图象分别交x轴,y轴于B点、A点,抛物线y=ax2+$\frac{1}{2}$x+c的图象经过A、B两点,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
如图,已知一次函数y=-$\frac{1}{2}$x+2的图象分别交x轴,y轴于B点、A点,抛物线y=ax2+$\frac{1}{2}$x+c的图象经过A、B两点,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.