题目内容
11.在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体=$\frac{4}{3}π{r}^{3}$,V圆锥=$\frac{1}{3}π{r}^{2}$h)(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
分析 (1)作斜边上的高分成两个直角三角形旋转即可;
(2)确定圆锥的高与半径即可求出体积;
(3)分别求出两种图形的体积,再比较即可.
解答 解:(1)两个圆锥形成的几何体;
(2)V圆锥=$\frac{1}{3}$πr2h=$\frac{1}{3}$π×82×6=128π,
(3)①如图$\frac{r}{8}$=$\frac{6}{10}$,解得r=$\frac{24}{5}$,
所以绕着斜边10所在的直线旋转一周形成的几何体的体积为V圆锥=$\frac{1}{3}$πr2h=$\frac{1}{3}$π×($\frac{24}{5}$)2×10=76.8π
②绕着直角边8所在的直线旋转一周形成的几何体的体积为V圆锥=$\frac{1}{3}$πr2h=$\frac{1}{3}$π×62×8=96π,
故绕着直角边8所在的直线旋转一周形成的几何体的体积大.
点评 本题考查将一个简单图形绕一轴旋转所组成的图形和圆锥体积计算方法,关键要弄清旋转后形成的圆锥的地面的半径和高,一般底面半径越大体积就越大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.函数y=$\frac{\sqrt{x-3}}{x-2}$的自变量x的取值范围是( )
| A. | x≠2 | B. | x≥3 | C. | x>3且x≠2 | D. | x≥3且x≠2 |
19.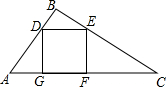 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )| A. | $\frac{6}{7}$ | B. | $\frac{30}{37}$ | C. | $\frac{12}{7}$ | D. | $\frac{60}{37}$ |
6.菱形的两条对角线分别是12cm和16cm,则菱形的边长为( )
| A. | 20cm | B. | 20 | C. | 10 | D. | 10cm |