题目内容
8.已知a+$\frac{1}{a}$=6,则a-$\frac{1}{a}$=$±4\sqrt{2}$.分析 根据a+$\frac{1}{a}$=6,可以求得${a}^{2}+\frac{1}{{a}^{2}}$的值,从而可以的得到a-$\frac{1}{a}$的值.
解答 解:∵$a+\frac{1}{a}=6$,
∴$(a+\frac{1}{a})^{2}={a}^{2}+2+\frac{1}{{a}^{2}}=36$,
∴${a}^{2}+\frac{1}{{a}^{2}}=34$,
∴$(a-\frac{1}{a})^{2}={a}^{2}-2+\frac{1}{{a}^{2}}=34-2=32$,
∴$a-\frac{1}{a}=±4\sqrt{2}$,
故答案为:$±4\sqrt{2}$.
点评 本题考查分式的混合运算,解题的关键是由a+$\frac{1}{a}$=6可以通过变形得到${a}^{2}+\frac{1}{{a}^{2}}$的值,从而建立与a-$\frac{1}{a}$的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.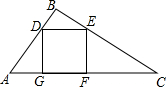 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )| A. | $\frac{6}{7}$ | B. | $\frac{30}{37}$ | C. | $\frac{12}{7}$ | D. | $\frac{60}{37}$ |
 如图所示,∠AOB=90°,OE,OC分别是∠AOD,∠DOB的平分线,则∠EOC=45°.
如图所示,∠AOB=90°,OE,OC分别是∠AOD,∠DOB的平分线,则∠EOC=45°.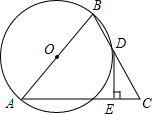 已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.
已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.