题目内容
9.m为何值时,方程2(m+1)x2+4mx+(2m-1)=0有两个不相等的实数根?分析 根据方程2(m+1)x2+4mx+(2m-1)=0有两个不相等的实数根得到2(m+1)≠0且△>0,列出m的不等式,求出m的取值范围即可.
解答 解:∵方程2(m+1)x2+4mx+(2m-1)=0有两个不相等的实数根,
∴2(m+1)≠0且△>0,即16m2-4×2(m+1)(2m-1)>0,
解得m<1,
∴m的取值范围为m<1且m≠-1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式,解答本题要掌握△>0,方程有两个不相等的实数根,此题很容易漏掉二次项系数不为0的情况,此题不是难题,但是很容易出现错误.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19.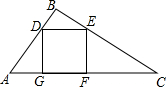 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
 有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )| A. | $\frac{6}{7}$ | B. | $\frac{30}{37}$ | C. | $\frac{12}{7}$ | D. | $\frac{60}{37}$ |
 如图,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是3<r≤4或r=$\frac{12}{5}$.
如图,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是3<r≤4或r=$\frac{12}{5}$.



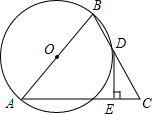 已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.
已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.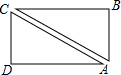 传说中愚公移山后,为了陶冶性情,在自家门前开了一个长方形人工湖,如图,愚公每次出门赶集,都要从家中A点出发,经过B或D点到集市C点,久而久之,他发观这样太浪费时间.于是决定在A,C之间修一条水上长廊,已知AD=8000米,CD=6000米,步行速度为4千米/时.问:长廊修好后,愚公每次去集市可节省多少时间?
传说中愚公移山后,为了陶冶性情,在自家门前开了一个长方形人工湖,如图,愚公每次出门赶集,都要从家中A点出发,经过B或D点到集市C点,久而久之,他发观这样太浪费时间.于是决定在A,C之间修一条水上长廊,已知AD=8000米,CD=6000米,步行速度为4千米/时.问:长廊修好后,愚公每次去集市可节省多少时间?