题目内容
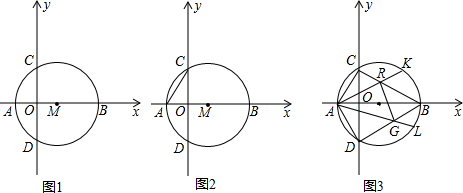
2.如图1:在平面直角坐标系xOy中,M为x轴正半轴上一点,⊙M与x轴交于A、B两点,与 y轴交于C、D两点,若点M的坐标为(2,0),B点的坐标为(6,0).(1)求C点的坐标;
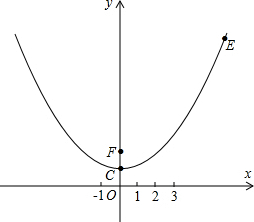
(2)如图2连接AC,若E为⊙M上一点,且弦AE长为$4\sqrt{2}$,求∠EAC的度数.
(3)如图3:K、L分别为 $\widehat{BC}$、$\widehat{BD}$上的动点,连接AK,BC交于点R,AL、BD交于点G,若∠KAL=60° 现给出两个结论:①△ARG的周长不变;②△BRG的周长不变.其中有一个结论正确,请选择正确结论并求值.
分析 (1)连接MC,由点M、B的坐标得出OM=2,OB=6,得出MB=4,MC=MA=4,由勾股定理求出OC,即可得出点C的坐标;
(2)分两种情况:①作MN⊥AE于N,由垂径定理得出AN,由勾股定理求出MN,得出∠MAN=45°,即可得出结果;
②同①求出∠MAN=45°,即可得出结果;
(3)延长BD到E,使DE=CR,连接AE,由垂径定理得出AC=AD,BC=BD,由勾股定理求出BC,由SAS证明△ACR≌△ADE,得出AR=AE,∠CAR=∠DAE,再证明△ARG≌△AEG,得出RG=EG,即可得出△BRG的周长.
解答 解:(1)连接MC,如图1所示: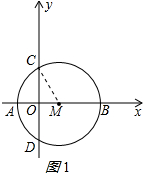 ∵M的坐标为(2,0),B点的坐标为(6,0),
∵M的坐标为(2,0),B点的坐标为(6,0),
∴OM=2,OB=6,
∴MB=4,
∴MC=MA=4,
∵∠COM=90°,
∴OC=$\sqrt{M{C}^{2}-O{M}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴点C的坐标为(0,2$\sqrt{3}$);
(2)分两种情况:①如图2所示: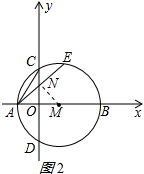
作MN⊥AE于N,则AN=EN=$\frac{1}{2}$AE=2$\sqrt{2}$,
∴MN=$\sqrt{M{A}^{2}-A{N}^{2}}$=2$\sqrt{2}$,
∴AN=MN,
∴∠MAN=45°,
∵OA=2,OC=2$\sqrt{3}$,∠AOC=90°,
∴tan∠OAC=$\frac{OC}{OA}=\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠OAC=60°,
∴∠EAC=∠OAC-MAN=15°;
②如图3所示:作MN⊥AE于N,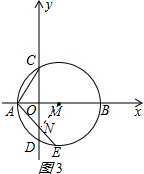
同①得出∠MAN=45°,
∴∠EAC=∠OAC+∠MAN=105°;
综上所述:∠EAC的度数为15°或105°;
(3)△BRG的周长不变,为8$\sqrt{3}$;理由如下:
延长BD到E,使DE=CR,连接AE,如图4所示:
∵AB是⊙M 的直径,AB⊥CD,
∴∠ACR=∠ADB=90°,$\widehat{AC}=\widehat{AD}$,$\widehat{BC}=\widehat{BD}$,
∴∠ADE=90°,AC=AD,BC=BD=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{6}^{2}}$=4$\sqrt{3}$,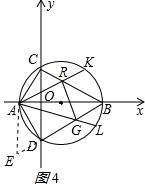
在△ACR和△ADE中,
$\left\{\begin{array}{l}{AC=AD}&{\;}\\{∠ACR=∠ADE=90°}&{\;}\\{CR=DE}&{\;}\end{array}\right.$,
∴△ACR≌△ADE(SAS),
∴AR=AE,∠CAR=∠DAE,
∵∠OAC=60°,
同理∠OAD=60°,
∵∠KAL=60°,
∴∠DAG=∠BAR,
∴∠EAG=∠OAC=∠KAL=60°,
在△ARG和△AEG中,
$\left\{\begin{array}{l}{AR=AE}&{\;}\\{∠RAG=∠EAG}&{\;}\\{AG=AG}&{\;}\end{array}\right.$,
∴△ARG≌△AEG(SAS),
∴RG=EG,
∴△BRG的周长=BR+BG+RG=BC+BD=2BC=8$\sqrt{3}$.
点评 本题是圆的综合题目,考查了勾股定理、圆周角定理、垂径定理、全等三角形的判定与性质、三角函数、等腰直角三角形的判定与性质等知识;本题难度较大,综合性强.特别是(2)中需要进行分类讨论,运用三角函数才能得出结果;(3)中需要通过作辅助线运用垂径定理、证明三角形全等才能得出结果.

| A. | 3(x-y)2+2(y-x)=(y-x)(3x-3y+2) | B. | 6(m+n)2-2(m+n)=(2m+n)(3m+n+1) | ||
| C. | -2a2+4a-2=-2(a+1)2 | D. | ab(a-b)-a(b-a)=-a(b-a)(b+1) |
 阅读材料:
阅读材料: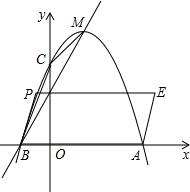 已知抛物线y=-x2+ax+b的顶点M(1,4),与x轴的一个交点A(3,0).
已知抛物线y=-x2+ax+b的顶点M(1,4),与x轴的一个交点A(3,0).