题目内容
4.给出如下两个方程,方程ax2-x-1=0①;方程a(ax2-1)2-x-1=0②;(1)证明方程①的实根都是方程②的实根;
(2)如果方程①和②的实根相同,求a的取值范围.
分析 (1)分类讨论:当a=0,它们的解都为1;当a≠0时,若方程①有实数解,由①得ax2-1=x,把ax2-1=x代入②得ax2-x-1=0,于是得到它们的解一样,然后综合两种情况即可;
(2)根据判别式的意义得到a≥-$\frac{1}{4}$.
解答 解:(1)当a=0,方程①变形为-x-1=0,解得x=-1;
方程②变形为-x-1=0,解得x=-1,它们的解相同;
由①得ax2-1=x,把ax2-1=x代入②得ax2-x-1=0,它们有相同的解,
∴方程①的实根都是方程②的实根;
(2)由(1)得:方程①的实根都是方程②的实根,
则△=1+4a≥0,解得a≥-$\frac{1}{4}$,
所以a的取值范围为a≥-$\frac{1}{4}$.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
相关题目
15.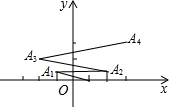 如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
 如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )| A. | (50,49) | B. | (51,50) | C. | (-50,49) | D. | (100,99) |
19.一个等腰三角形的一边长是6,另一边长是8.那么这个等腰三角形的周长是( )
| A. | 20 | B. | 20或24 | C. | 22 | D. | 20或22. |
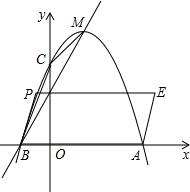 已知抛物线y=-x2+ax+b的顶点M(1,4),与x轴的一个交点A(3,0).
已知抛物线y=-x2+ax+b的顶点M(1,4),与x轴的一个交点A(3,0).