题目内容
已知下面四个图中AB∥CD,试探讨四个图形中∠APC与∠PAB﹑∠PCD的数量关系.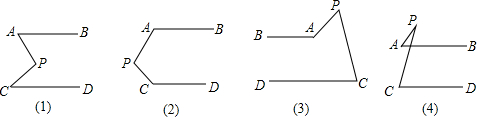
(1)图(1)中∠APC与∠PAB﹑∠PCD的关系是 .
(2)图(2)中∠APC与∠PAB﹑∠PCD的关系是 .
(3)请你在图(3)和图(4)中任选一个,说出∠APC与∠PAB﹑∠PCD的关系,并加以证明.(提示:可过P点作PE∥AB)
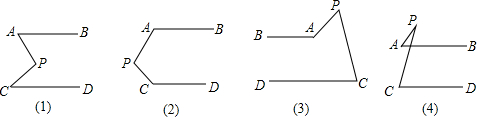
(1)图(1)中∠APC与∠PAB﹑∠PCD的关系是
(2)图(2)中∠APC与∠PAB﹑∠PCD的关系是
(3)请你在图(3)和图(4)中任选一个,说出∠APC与∠PAB﹑∠PCD的关系,并加以证明.(提示:可过P点作PE∥AB)
考点:平行线的性质
专题:
分析:(1)过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,内错角相等可得∠PAB=∠APE,∠PCD=∠CPE,然后根据∠APC=∠APE+∠CPE整理即可;
(2)过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,同旁内角互补∠PAB+∠APE=180°,∠PCD+∠CPE=180°,然根据∠APC=∠APE+∠CPE整理即可;
(3)图(3)过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,同旁内角互补∠PAB+∠APE=180°,∠PCD+∠CPE=180°,然根据∠APC=∠CPE-∠APE整理即可.
(2)过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,同旁内角互补∠PAB+∠APE=180°,∠PCD+∠CPE=180°,然根据∠APC=∠APE+∠CPE整理即可;
(3)图(3)过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,同旁内角互补∠PAB+∠APE=180°,∠PCD+∠CPE=180°,然根据∠APC=∠CPE-∠APE整理即可.
解答:解:(1)如图,过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB=∠APE,∠PCD=∠CPE,
∵∠APC=∠APE+∠CPE,
∴∠APC=∠PAB+∠PCD;
(2)过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°,
∵∠APC=∠APE+∠CPE,
∴∠APC+∠PAB+∠PCD=360°;
故答案为:(1)∠APC=∠PAB+∠PCD;
(2)∠APC+∠PAB+∠PCD=360°;
(3)图(3)过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°,
∵∠APC=∠CPE-∠APE,
∴∠APC=∠PAB-∠PCD;
同理图(4)∠APC=∠PCD-∠PAB.
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB=∠APE,∠PCD=∠CPE,

∵∠APC=∠APE+∠CPE,
∴∠APC=∠PAB+∠PCD;
(2)过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°,
∵∠APC=∠APE+∠CPE,
∴∠APC+∠PAB+∠PCD=360°;
故答案为:(1)∠APC=∠PAB+∠PCD;
(2)∠APC+∠PAB+∠PCD=360°;
(3)图(3)过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°,
∵∠APC=∠CPE-∠APE,
∴∠APC=∠PAB-∠PCD;
同理图(4)∠APC=∠PCD-∠PAB.
点评:本题考查了平行线的性质,熟记性质是解题的关键,此类题目难点在于过拐点作平行线.

练习册系列答案
相关题目
下列关系式中,正确的是( )
| A、(a-b)2=a2-b2 |
| B、(a+b)(a-b)=a2+b2 |
| C、(a+b)2=a2+b2 |
| D、(a+b)2=a2+2ab+b2 |
 如图,在平行四边形ABCD中,AC=12cm,BD=6cm,求AD的长和四边形的面积.
如图,在平行四边形ABCD中,AC=12cm,BD=6cm,求AD的长和四边形的面积. 如图是某市部分地区的示意图,请你建立适当的平面直角坐标系,并写出图中各地点相应的坐标.
如图是某市部分地区的示意图,请你建立适当的平面直角坐标系,并写出图中各地点相应的坐标.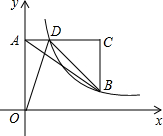 如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数y=
如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数y= 如图,AB=AC,AE是△ABC中BC边上的高线,点D在直线AE上一点(不与A、E重合).
如图,AB=AC,AE是△ABC中BC边上的高线,点D在直线AE上一点(不与A、E重合).