题目内容
1. 如图,等边△ABC中,AB=4,O为三角形中心,⊙O的直径为1,现将⊙O沿某一方向平移,当它与等边△ABC的某条边相切时停止平移,记平移的距离为d,则d的取值范围是$\frac{2}{3}\sqrt{3}$-$\frac{1}{2}$≤d≤$\frac{4}{3}\sqrt{3}$-1.
如图,等边△ABC中,AB=4,O为三角形中心,⊙O的直径为1,现将⊙O沿某一方向平移,当它与等边△ABC的某条边相切时停止平移,记平移的距离为d,则d的取值范围是$\frac{2}{3}\sqrt{3}$-$\frac{1}{2}$≤d≤$\frac{4}{3}\sqrt{3}$-1.
分析 如图所示,当圆心运动到与点P重合时,d最大,运动到与点Q重合时,d最小,求出OP与OQ,即可确定出d的范围.
解答  解:如图1,PF⊥AB于F,OE⊥AB于E,
解:如图1,PF⊥AB于F,OE⊥AB于E,
等边△ABC中,AB=4,则AE=$\frac{1}{2}$AB=2,
则OA=$\frac{4}{3}\sqrt{3}$,
∵PF=$\frac{1}{2}$,
∴AP=1,
∴OP=$\frac{4}{3}\sqrt{3}$-1,
如图2,AH=$\frac{1}{2}$AB=2,∠OAH=30°,
∴OH=$\frac{2}{3}\sqrt{3}$,
QH=$\frac{1}{2}$,
∴OQ=$\frac{2}{3}\sqrt{3}$-$\frac{1}{2}$,
∴$\frac{2}{3}\sqrt{3}$-$\frac{1}{2}$≤d≤$\frac{4}{3}\sqrt{3}$-1.
点评 此题考查了切线的性质,勾股定理,以及等边三角形的性质,找出d的最大值与最小值是解本题的关键.

练习册系列答案
相关题目
11.将抛物线y=2x2+1向左平移1个单位,再向下平移3个单位后所得到的抛物线为( )
| A. | y=2(x+1)2-2 | B. | y=2(x+1)2+4 | C. | y=2(x-1)2-2 | D. | y=2(x-1)2+4 |
9.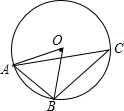 如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
 如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )| A. | π | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
6.将抛物线y=(x-1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
| A. | y=(x-2)2 | B. | y=x2 | C. | y=x2+6 | D. | y=(x-2)2+6 |
10.下列实数中,是无理数的是( )
| A. | -1 | B. | 0 | C. | $\sqrt{2}$ | D. | 3.14 |