题目内容
13．解不等式组：$\left\{\begin{array}{l}{9x+5＜8x+7}\\{\frac{4}{3}x+2＞1-\frac{2}{3}x}\end{array}\right.$的整数解是0，1．分析 分别求出不等式组中两不等式的解集，找出两解集的公共部分确定出不等式组的解集，进而确定出不等式组的整数解即可．
解答 解：$\left\{\begin{array}{l}{9x+5＜8x+7①}\\{\frac{4}{3}x+2＞1-\frac{2}{3}x②}\end{array}\right.$，
由①得：x＜2；
由②得：x＞-$\frac{1}{2}$，
∴不等式组的解集为-$\frac{1}{2}$＜x＜2，
则不等式组的整数解为0，1．
故答案为：0，1．
点评 此题考查了一元一次不等式组的整数解，熟练掌握运算法则是解本题的关键．
练习册系列答案
优加精卷系列答案
相关题目
3．?|-2|等于（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | ±$\frac{1}{2}$ |
4．花粉的质量很小，一粒某种花粉的质量约为0.000103毫克，那么0.000103可用科学记数法表示为（ ）
| A． | 10.3×10-5 | B． | 1.03×10-4 | C． | 0.103×10-3 | D． | 1.03×10-3 |
如图，等边△ABC中，AB=4，O为三角形中心，⊙O的直径为1，现将⊙O沿某一方向平移，当它与等边△ABC的某条边相切时停止平移，记平移的距离为d，则d的取值范围是$\frac{2}{3}\sqrt{3}$-$\frac{1}{2}$≤d≤$\frac{4}{3}\sqrt{3}$-1．
8．
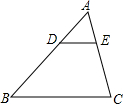如图，在△ABC中，DE∥BC，若AD=1，DB=2，则$\frac{DE}{BC}$的值为（ ）
如图，在△ABC中，DE∥BC，若AD=1，DB=2，则$\frac{DE}{BC}$的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
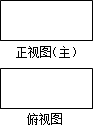如图，某立体的正视图和俯视图是长、宽分别相等的矩形，给定下列三个命题：
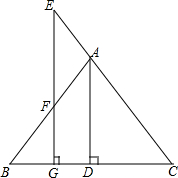已知：如图，△ABC中，AD⊥BC于D，E是CA延长线上一点，EG⊥BC于G，交AB于F，AD是∠BAC的角平分线，试说明∠E=∠EFA．