题目内容
16.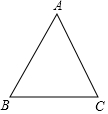 如图,△ABC是等腰三角形,AB=AC.
如图,△ABC是等腰三角形,AB=AC.(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①以AB为直径作图,圆心为O,⊙O与BC、AC分别交于点D、E;
②连接ED,作∠EDC的平分线,与AC交于点F.
(2)综合与运用:在你所作的图中,若AE=7,BC=6,则:
①FD与⊙O的位置关系是相切,并加以证明.
②线段AC的长为9.
分析 (1)①作AB的中垂线找到AB中点O,再作圆即可得;②根据角平分线的作图可得;
(2)根据等腰三角形的性质可知AD⊥BC、BD=CD=DE,由∠EDF=∠CDF知DF⊥AC,根据OD为△ABC中位线可得OD⊥DF,得证;②设⊙O的半径为r,得出AC=2r、CF=r-$\frac{7}{2}$、CD=3,证△DFC∽△ADC得$\frac{CF}{CD}$=$\frac{CD}{CA}$,据此求得r的值即可得出答案.
解答 解:(1)①如图,⊙O即为所求;
②DF即为所求;
(2)①相切,
如图,连接OD、AD,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
又∵AB=AC,
∴BD=CD,∠BAD=∠CAD,
∴BD=DE,
∴DE=DC,
∵∠EDF=∠CDF,
∴DF⊥AC,
∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC,
∴OD⊥DF,即DF为⊙O的切线,
故答案为:相切;
②设⊙O的半径为r,则AB=AC=2r,EC=AC-AE=2r-7,
∵DE=DC,且∠EDF=∠CDF,
∴CF=$\frac{1}{2}$EC=r-$\frac{7}{2}$,
∵BC=6,
∴BD=DE=DC=3,
∵∠DFC=∠ADC=90°,∠C=∠C,
∴△DFC∽△ADC,
∴$\frac{CF}{CD}$=$\frac{CD}{CA}$,即$\frac{r-\frac{7}{2}}{3}$=$\frac{3}{2r}$,
解得:r=-1(舍)或r=$\frac{9}{2}$,
∴AC=2r=9,
故答案为:9
点评 本题主要考查作图-复杂作图,熟练掌握基本的尺规作图和等腰三角形的性质、圆周角定理、相似三角形的判定与性质是解题的关键.

练习册系列答案
相关题目
1.在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,cosA的值的变化情况是( )
| A. | 不断变大 | B. | 不断减小 | C. | 不变 | D. | 不能确定 |
8.观察下列各图,图中的小正方形是按一定的规律排列,根据此规律,第10个图中小正方形的个数为( )

| A. | 80 | B. | 81 | C. | 82 | D. | 83 |
6. 如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )
如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )
 如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )
如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )| A. | 110° | B. | 115° | C. | 130° | D. | 135° |
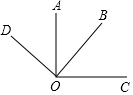 如图所示,∠AOB=42°,OA⊥OC,OB⊥OD,则∠COD=138°.
如图所示,∠AOB=42°,OA⊥OC,OB⊥OD,则∠COD=138°. 平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.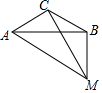 如图,在△ABC中,∠ACB=120°,点M为△ABC外一点,且∠AMB=60°,若CM平分∠AMB.求证:AM+BM=$\sqrt{3}$CM.
如图,在△ABC中,∠ACB=120°,点M为△ABC外一点,且∠AMB=60°,若CM平分∠AMB.求证:AM+BM=$\sqrt{3}$CM.