题目内容
11.对于函数y=$\frac{6}{x}$,下列说法错误的是( )| A. | 它的图象分布在第一、三象限 | B. | 它的图象与直线y=-x无交点 | ||
| C. | 当x>0时,y的值随x的增大而增大 | D. | 当x<0时,y的值随x的增大而减小 |
分析 根据反比例函数的性质对四个选项进行逐一分析即可.
解答 解:A、∵函数y=$\frac{6}{x}$中k=6>0,∴此函数图象的两个分支分别在一、三象限,故本选项正确;
B、∵函数y=$\frac{6}{x}$的图象位于一、三象限,y=-x经过二、四象限,∴两函数图象无交点,故本选项正确;
C、∵当x>0时,函数的图象在第一象限,∴y的值随x的增大而减小,故本选项错误;
D、∵当x<0时,函数的图象在第三象限,∴y的值随x的增大而减小,故本选项正确.
故选C.
点评 本题考查的是反比例函数的性质,即反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线,当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
19.下列各点,在函数y=2x-3的图象上的是( )
| A. | (1,1) | B. | (-1,5) | C. | (-2,-7) | D. | (-$\frac{3}{2}$,0) |
3.计算$\sqrt{12}$-$\sqrt{\frac{3}{4}}$的结果正确的是( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{8}$ | D. | 0 |
1.一个正方形的面积是10,估计它的边的长度在( )
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
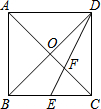 如图,在边长为2的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则EF的长为$\frac{\sqrt{5}}{3}$.
如图,在边长为2的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则EF的长为$\frac{\sqrt{5}}{3}$. 如图,CD平分∠ACB,且CD∥AE,如果∠ACE=80°.求∠CAE.
如图,CD平分∠ACB,且CD∥AE,如果∠ACE=80°.求∠CAE.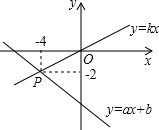 如图,已知函数y=ax+b和y=kx的图象交于点P,根据图象可直接得关于x的不等式ax+b≥kx的解集是x≤-4.
如图,已知函数y=ax+b和y=kx的图象交于点P,根据图象可直接得关于x的不等式ax+b≥kx的解集是x≤-4.