题目内容
17.解方程(1)$\frac{x}{x-2}$-1=$\frac{8}{{x}^{2}-4}$
(2)$\frac{x}{x+1}$=$\frac{2x}{3x+3}$+1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x2+2x-x2+4=8,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:3x=2x+3x+3,
解得:x=-$\frac{3}{2}$,
经检验x=-$\frac{3}{2}$是分式方程的解.
点评 此题考查了解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.计算(3a2b3)3正确的结果是( )
| A. | 27a6b9 | B. | 27a8b27 | C. | 9a6b9 | D. | 27a5b6 |
5.算式:(-4)-2的计算结果是( )
| A. | -16 | B. | $\frac{1}{16}$ | C. | 16 | D. | $-\frac{1}{16}$ |
6. 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
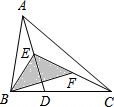 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.
如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积. 如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)
如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)