题目内容
14.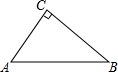 如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
分析 直接利用点到直线的距离以及三角形面积求法分别得出答案.
解答 解:∠ACB=90°,即AC⊥BC,
若BC=8cm,AC=6cm,AB=10cm,
那么B到AC的距离是:8cm,A到BC的距离是:6cm,
A,B两点间的距离为:10cm,C到AB的距离是:$\frac{6×8}{10}$=4.8(cm).
故答案为:⊥,8cm,6cm,10cm,4.8cm.
点评 此题主要考查了点到直线的距离,正确结合三角形面积求出C到AB的距离是解题关键.

练习册系列答案
相关题目
19.据有关资料,当前我国的道路交通安全形势十分严峻,去年我国交通事故的伤亡人数约为20.4万人,居世界第一.则数20.4万用科学记数法表示是( )
| A. | 2.04×104 | B. | 2.04×105 | C. | 2.04×106 | D. | 20.4×104 |
5.下面给出了四边形ABCD的四内角关系中,能说明它是平行四边形的是( )
| A. | 1:2:3:4 | B. | 2:3:2:3 | C. | 2:2:3:3 | D. | 2:3:3:2 |
2.估算$\sqrt{18}$的值是在( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
6.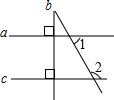 如图,已知在同一平面内的三条直线a,b,c,且a⊥b,b⊥c,若∠1=55°,则∠2的度数为( )
如图,已知在同一平面内的三条直线a,b,c,且a⊥b,b⊥c,若∠1=55°,则∠2的度数为( )
 如图,已知在同一平面内的三条直线a,b,c,且a⊥b,b⊥c,若∠1=55°,则∠2的度数为( )
如图,已知在同一平面内的三条直线a,b,c,且a⊥b,b⊥c,若∠1=55°,则∠2的度数为( )| A. | 55° | B. | 125° | C. | 135° | D. | 无法确定 |
4.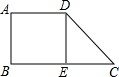 如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
 如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )| A. | 24 | B. | 8$\sqrt{3}$ | C. | 36 | D. | 48 |