题目内容
13.九年级数学兴趣小组经过市场调查,得到某种运动服进价为每件60元,每月的销量与售价的相关信息如表:| 售价x(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量y(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示:①销售该运动服每件的利润是(x-60)元,②月销量是(-2x+400)件.(直接写出结果);
(2)若要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?
(3)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
分析 (1)根据利润=售价-进价求出利润,运用待定系数法求出月销量;
(2)根据月利润=每件的利润×月销量=8000列方程,解方程即可;
(3)根据月利润=每件的利润×月销量列出函数关系式,根据二次函数的性质求出最大利润
解答 解:(1)①销售该运动服每件的利润是(x-60)元;
②设月销量W与x的关系式为w=kx+b,
由题意得,$\left\{\begin{array}{l}{100k+b=200}\\{110k+b=180}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-2}\\{b=400}\end{array}\right.$,
∴W=-2x+400,
故答案为:x-60-2x+400;
(2)由题意可知:(x-60)(-2x+400)=8000,
即-2x2+520x-24000=8000,
解得:x=160或100,
当x=160时,销售成本为4800<10000,符合要求,
当x=100时,销售成本为12000>10000,不符合要求,
∴月销售利润达到8000元,销售单价应定为160元;
(3)由题意得,y=(x-60)(-2x+400),
=-2x2+520x-24000,
=-2(x-130)2+9800,
∴售价为130元时,当月的利润最大,最大利润是9800元.
点评 本题考查的是二次函数的应用,、一次函数的运用以及解一元二次方程,掌握待定系数法求函数解析式和二次函数的性质以及最值的求法是解题的关键.

练习册系列答案
相关题目
4.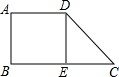 如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
 如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )| A. | 24 | B. | 8$\sqrt{3}$ | C. | 36 | D. | 48 |
8.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物,将0.0000025用科学记数法表示为( )
| A. | 2.5×10-5 | B. | 2.5×10-6 | C. | 0.25×10-5 | D. | 2.5×106 |
18.下列命题
①直径是弦;
②平分弦的直径垂直于弦;
③若两段弧的度数相等,则它们是等弧;
④三角形的内心到三角形的三个顶点的距离相等;
⑤圆的切线垂直于过切点的半径.
正确的有( )
①直径是弦;
②平分弦的直径垂直于弦;
③若两段弧的度数相等,则它们是等弧;
④三角形的内心到三角形的三个顶点的距离相等;
⑤圆的切线垂直于过切点的半径.
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.(-2)-3的值等于( )
| A. | 6 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |