题目内容
8.某公司生产一种产品,每件产品成本价是400元,销售价为510元,第一季度销售了5000件.(1)求该产品第一季度的销售总利润(销售利润=销售价-成本价)是多少元?
(2)为进一步扩大市场,公司决定降低生产成本,经过市场调研,在降低生产成本后,第二季度这种产品每件销售价降低了4%,销售量比第一季度提高了10%,销售总利润比第一季度提高了20%.求该产品每件的成本价降低了多少元?
分析 (1)用每件的利润乘以第一季度销售量5000件即可得到第一季度的销售总利润;
(2)设该产品每件的成本价降低了x元,则第二季度的成本为(400-x)元,第二季度每件销售价为510(1-4%),第二季度的销售量为5000•(1+10%),然后利用第二季度的销售总利润比第一季度提高了20%列方程得[510×(1-4%)-(400-x)]•5000•(1+10%)=550000•(1+20%),再解方程即可.
解答 解:(1)5000×(510-400)=550000(元).
答:该产品第一季度的销售总利润是550000元;
(2)设该产品每件的成本价降低了x元,
根据题意得[510×(1-4%)-(400-x)]•5000•(1+10%)=550000•(1+20%),
解得x=30.4(元).
答:该产品每件的成本价降低了30.4元.
点评 本题考查了解一元一次方程的应用::首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.解决本题的关键是表示出第二季度每件得销售价和成本.

练习册系列答案
相关题目

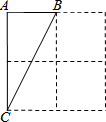 如图,在2×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.
如图,在2×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.
 如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为75或81.
如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为75或81.