题目内容

6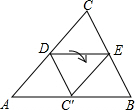．如图，D、E分别为△ABC的AC，BC边的中点，将△CDE沿DE折叠，使点C落在AB边上的点C′处，若∠CDE=35°，则∠AC′D等于（　　）
A．35°B．55°C．70°D．110°

分析 先根据图形翻折不变性的性质可得：∠C'DE=∠CDE=35°，再由DE是三角形的中位线，则DE∥AB，根据平行线的性质求解．

解答 解：∵∠C'DE=∠CDE=35°，
又∵D、E分别为△ABC的AC，BC边的中点，
∴DE∥AB，
∴∠AC'D=∠C'DE=35°．
故选A．

点评 本题考查的是图形翻折变换的性质及三角形的中位线的性质，熟知折叠的性质是解答此题的关键．

练习册系列答案
相关题目
16．解下列方程：
①x2-4x-6=0；
②3x（x+2）=5（x+2）．
17．-5$\frac{2}{3}$和1之间的负整数有-5，-4，-3，-2，-1．
14．下列各方程中，不是一元一次方程的是（　　）
A．x-2=2x+1B．y+5=7-yC．3x+$\frac{1}{x}$=2D．4-2y=$\frac{1}{2}$y
1．直线y=x+3上有一点P（m，2），则P点关于原点的对称点P′的坐标为（1，-2）．
11．某汽车经销商根据市场需求，计划购进某品牌A、B两种型号的汽车，如果分别购进A、B两种型号的汽车3辆、5辆，那么共需要111万元；如果分别购进A、B两种型号的汽车6辆、8辆，那么共需要192万元．
（1）A、B两种型号的汽车每辆多少万元？
（2）如果该经销商计划购进A、B两种型号的汽车共50辆，所用资金不超过650万元，且A种型号的汽车不多于36辆，那么有几种购买方案？
（3）在（2）的情况下，如果A型号的汽车加价15%，B型号的汽车加价16%出售，且所购汽车均全部售出，那么该经销商使用哪种方案可获得最大利润？最大利润是多少？
18．如果a＞0，且a的倒数等于它本身，b是最大的负整数．
（1）求（a+b）3×（$\frac{b}{a}$）3-2012的值；
（2）若x为负数，化简|a-x|+|b+x|+|x|；
（3）计算
$\frac{1}{a+1}+（\frac{1}{a+2}+\frac{2}{a+2}）$+（$\frac{1}{a+3}+\frac{2}{a+3}+\frac{3}{a+3}$）+（$\frac{1}{a+4}+\frac{2}{a+4}+\frac{3}{a+4}+\frac{4}{a+4}$）+…+（$\frac{1}{a+29}+\frac{2}{a+29}+\frac{3}{a+29}+…+\frac{29}{a+29}$）．（提示：1+2+3+…+29=435）
15．线段AB长10cm，点P在线段AB上，且满足$\frac{BP}{AP}$=$\frac{AP}{AB}$，那么AP的长为5$\sqrt{5}$-5cm．
16．等腰△ABC中，AB=AC=5，BC=8，则底角∠B的正切值是$\frac{3}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网