题目内容
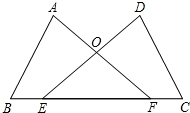
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)若∠EOF=60°试判断△OEF的形状,并说明理由.
【考点】全等三角形的判定与性质;等边三角形的判定与性质.
【分析】(1)易证BF=CE,即可求得△ABF≌△DCE,即可解题;
(2)根据(1)中求证的△ABF≌△DCE,即可求得∠OEF=∠OFE,即可解题.
【解答】解:(1)∵BE=CF,
∴BF=CE,
在△ABF和△DCE中,
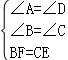 ,
,
∴△ABF≌△DCE,(AAS)
∴AB=DC;
(2)∵△AB F≌△DCE,
F≌△DCE,
∴∠OEF=∠OFE,
∵∠EOF=60°,
∴∠OEF=∠OFE=∠EOF=60°,
∴△OEF为等边三角形.
【点评】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,考查了等边三角形的判定,本题中求证△ABF≌△DCE是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目