题目内容
11．因式x2+ax+b时，甲看错了a的值，分解的结果是（x+6）（x-1），乙看错了b，分解的结果是（x-2）（x+1），那么ab=6．分析 根据x2+（p+q）x+pq型的式子的因式分解特点即可得出答案．甲看错了a的值，分解的结果为（x+6）（x-1），而b值不错可求出b的准确值，同理求出a的准确值．
解答 解：因为甲看错了a的值，分解的结果为（x+6）（x-1）=x2+5x-6，
所以b=-6，
又因为乙看错了b的值，分解的结果是（x-2）（x+1）=x2-x-2，
所以a=-1，
所以ab=（-6）×（-1）=6．
故答案是：=6．
点评 主要考查了二次三项式的分解因式．掌握此类式子的特点可以使计算简便．
练习册系列答案
相关题目
3．
把边长相等的正五边形和正六边形按照如图的方式叠合在一起，AB是正六边形的对角线，则∠α等于（ ）
把边长相等的正五边形和正六边形按照如图的方式叠合在一起，AB是正六边形的对角线，则∠α等于（ ）| A． | 72° | B． | 84° | C． | 88° | D． | 90° |
20．
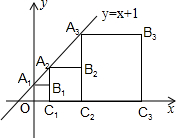正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点Bn的坐标是（ ）
正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点Bn的坐标是（ ）| A． | （2n-1，2n-1） | B． | （2n-1，2n-1） | C． | （2n，2n-1） | D． | （2n-1，2n） |
在平面直角坐标系xOy中，已知抛物线y=a（x+1）2+c（a＞0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，其顶点为M，若直线MC的函数表达式为y=kx-3，与x轴的交点为N，且cos∠BCO=$\frac{3\sqrt{10}}{10}$．