题目内容
3. 把边长相等的正五边形和正六边形按照如图的方式叠合在一起,AB是正六边形的对角线,则∠α等于( )
把边长相等的正五边形和正六边形按照如图的方式叠合在一起,AB是正六边形的对角线,则∠α等于( )| A. | 72° | B. | 84° | C. | 88° | D. | 90° |
分析 根据正五边形的内角和和正六边形的内角和公式求得正五边形的内角108°和正六边形的内角120°,然后根据四边形的内角和即可得到结论.
解答  解:∵正五边形的内角=108°,正六边形的内角=120°,
解:∵正五边形的内角=108°,正六边形的内角=120°,
∵AB是正六边形的对角线,
∴∠1=∠2=60°,
∴∠α=360°-2×108°-120°=84°,
故选B.
点评 本题考查了多边形的内角与外角,熟练正五边形的内角,正六边形的内角,四边形的内角和公式是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
13.(5x2-4y2)(-5x2+4y2)运算的结果是( )
| A. | -25x4-16y4 | B. | -25x4+40x2y2-16y4 | ||
| C. | 25x4-16y4 | D. | 25x4-40x2y2+16y4 |
14.在Rt△ABC中,∠C=90°,tanA=$\frac{4}{3}$,则cosB的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
15.在△ABC中,∠C=60°,∠B=70°,则∠A的度数是( )
| A. | 70° | B. | 55° | C. | 50° | D. | 40° |
12.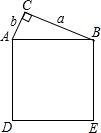 已知:如图,△ACB的面积为30,∠C=90°,BC=a,AC=b,正方形ADEB的面积为169,则(a-b)2的值为( )
已知:如图,△ACB的面积为30,∠C=90°,BC=a,AC=b,正方形ADEB的面积为169,则(a-b)2的值为( )
 已知:如图,△ACB的面积为30,∠C=90°,BC=a,AC=b,正方形ADEB的面积为169,则(a-b)2的值为( )
已知:如图,△ACB的面积为30,∠C=90°,BC=a,AC=b,正方形ADEB的面积为169,则(a-b)2的值为( )| A. | 25 | B. | 49 | C. | 81 | D. | 100 |
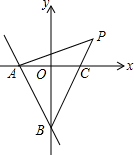 如图,在平面直角坐标系中,点P的坐标为(3,2),若直线y=-2x-4与x轴、y轴分别交于A、B两点,连接PA、PB.
如图,在平面直角坐标系中,点P的坐标为(3,2),若直线y=-2x-4与x轴、y轴分别交于A、B两点,连接PA、PB. 如图,在△ABC中,∠B=30°,BC的垂直平分线交边AB于E,垂足为D,连接CE,若ED=3,则CE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交边AB于E,垂足为D,连接CE,若ED=3,则CE的长为( )