题目内容
3.我们把符号“n!”读作“n的阶乘”.规定1:“n为自然数,当n≠0时,n!=n•(n-1)•(n-2)•…•2•1,当n=0时,0!=1.”例如:6!=6×5×4×3×2×1=720.
规定2:“在含有阶乘和加、减、乘、除运算时,应先计算阶乘,再乘除,后加减,有括号就先算括号里面的”.
按照以上的定义和运算顺序,计算:
(1)4!;
(2)$\frac{0!}{2!}$;
(3)(3+2)!-4!;
(4)用具体数试验一下,看看等式(m+n)!=m!+n!是否恒成立.
分析 (1)根据题意4!=4×3×2×1=24;
(2)根据规定2,$\frac{0!}{2!}$=$\frac{1}{2×1}$=$\frac{1}{2}$;
(3)根据规定2,(3+2)!-4!=5!-4!,再运算即可;
(4)用赋值法证明即可;
解答 解:(1)4!=4×3×2×1=24;
(2)$\frac{0!}{2!}$=$\frac{1}{2×1}$=$\frac{1}{2}$;
(3)(3+2)!-4!=5!-4!=5×4×3×2×1-4×3×2×1=120-24=96;
(4)不成立.
如:m=3,n=2时,
3!=3×2×1=6,2!=2,
m!+n!=3!+2!=6+2=8,
(m+n)!=5!=120,
∴(m+n)!=m!+n!不成立.
点评 本题主要考查了数字的变化规律,根据题意发现规律,运用规律是解答此题的关键.

练习册系列答案
相关题目
12.在平面直角坐标系中,在第二象限的点是( )
| A. | (2,1) | B. | (2,-1) | C. | (-2,-1) | D. | (-2,1) |

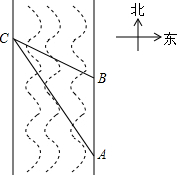 在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这段河段的宽度.(参考数值:tan31°≈$\frac{3}{5}$)
在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这段河段的宽度.(参考数值:tan31°≈$\frac{3}{5}$) 先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)