题目内容
如图是石景山当代商场地下广场到地面广场的手扶电梯示意图．其中AB、CD分别表示地下广场、地面广场电梯口处的水平线．已知∠ABC=135°，BC的长约是6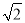
m，则乘电梯从点B到点C上升的高度h是_________．
6m
【解析】试题分析：
过点C作CM⊥AB交AB的延长线于点M, 由∠ABC=135°可得∠CBM=45°，在Rt△BMC中，由锐角三角函数即可求得CM=6．
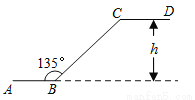
寒假天地重庆出版社系列答案如图，点A1、A2、A3、…、An在抛物线y=x2图象上，点B1、B2、B3、…、Bn在y轴上，若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形（点B0是坐标原点），则△A2015B2014B2015的腰长=____
2015
【解析】作A1C⊥y轴，A2E⊥y轴，垂足分别为C、E．
∵△A1BOB1、△A2B1B2都是等腰直角三角形
∴B1C=B0C=DB0=A1D，B2E=B1E=A2E
∴设A1（a，a）将其代入解析式y=x2得：
∴a=a2
解得：a=0（不符合题意）或a=1，由勾股定理得：A1B0=
同理可以求得：A2B1=2
A3B2=3
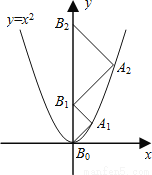
A4B... 某商场购进一种每件价格为100元的新商品，在商场试销发现：销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系：
(1)求出y与x之间的函数关系式；
(2)写出每天的利润W与销售单价x之间的函数关系式；若你是商场负责人，会将售价定为多少，来保证每天获得的利润最大，最大利润是多少？
（1）y＝－x＋180；（2）售价定为140元/件时，每天最大利润W＝1600元．
【解析】（1）设y与x之间的函数关系式为y=kx+b（k≠0），根据所给函数图象列出关于kb的关系式，求出k、b的值即可；
（2）把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式，由此关系式即可得出结论．
【解析】
（1）设y与x之间的函数关系式为y=kx+b（k≠0），由所给... 如图，在平面直角坐标系中，抛物线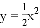
经过平移得到抛物线
，其对称轴与两段抛物线所围成的阴影部分的面积为
A. 2 B. 4 C. 8 D. 16
B
【解析】试题解析：过点C作CA⊥y，
∵抛物线y=x2-2x=（x2-4x）=（x2-4x+4）-2=（x-2）2-2，
∴顶点坐标为C（2，-2），
对称轴与两段抛物线所围成的阴影部分的面积为：2×2=4，
故选B． 小明乘滑草车沿坡比为1：2.4的斜坡下滑130米，求他下降的高度
50米
【解析】试题分析：根据坡比可设BC=x，AC=2.4x，根据勾股定理得出AB=2.6x，根据AB的长度得出x的值，从而得出BC的值，即下降的高度．
试题解析：∵坡比为1：2.4， ∴BC：AC=1：2.4， 设BC=x，AC=2.4x，
则AB= ∵AB=130米， ∴x=50， 则BC=x=50（米）． 身高相同的三个小朋友甲、乙、丙放风筝，他们放出的线长分别为300m，250 m，200m；线与地面所成的角度分别为30°，45°，60°(假设风筝线是拉直的)，则三人所放的风筝（ ）
A．甲的最高 B．乙的最低 C．丙的最低 D．乙的最高
D．
【解析】
试题解析：甲放的高度为：300×sin30°=150米．
乙放的高度为：250×sin45°=125≈176.75米．
丙放的高度为：200×sin60°=100≈173.2米．
所以乙的最高．
故选D． 一斜坡长为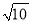
米，高度为1米，那么坡比为（ ）
A. 1：3 B. 1：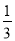 
C. 1： 
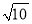D. 1：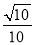 
A
【解析】试题分析：根据斜坡的长度和高度可以得出斜坡的水平距离为3米，则坡比=垂直高度：水平距离=1：3，故选A． 若y＝(m2－3m)x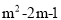
是二次函数，则m＝____．
-1
【解析】由二次函数的定义可知自变量的最高指数为2，且系数不等于0，可得m2－3m≠0，且；解得m=-1或m=3；当m=3时，m2－3m=0；最终可求得m=-1．
故答案为：-1. 下列各式从左到右的变形（1）15x2y=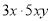
；（2）(x+y)(x-y)=x2-y2；
（3）x2-6x+9=(x-3)2；（4）x2+4x+1=x(x+4+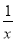
)，其中是因式分解的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式.根据因式分解的定义可得只有（3）符合要求，故选A.