题目内容
关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1,(a,m,b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是
x3=﹣4,x4=﹣1 .
考点: 一元二次方程的解.
专题: 计算题;压轴题.
分析: 把后面一个方程中的x+2看作整体,相当于前面一个方程中的x求解.
解答: 解:∵关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1,(a,m,b均为常数,a≠0),
∴方程a(x+m+2)2+b=0变形为a[(x+2)+m]2+b=0,即此方程中x+2=﹣2或x+2=1,
解得x=﹣4或x=﹣1.
故答案为:x3=﹣4,x4=﹣1.
点评: 此题主要考查了方程解的定义.注意由两个方程的特点进行简便计算.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
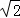 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为.
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为.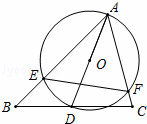
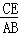 =
= ,则CF的长为 .
,则CF的长为 .

 B.
B.  C.
C.  D.
D. 