题目内容
如图，E是▱ABCD的边CD上一点，连接AE并延长交BC的延长线于点F，且AD=4，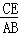
=
，则CF的长为 ．
2
考点： 相似三角形的判定与性质；平行四边形的性质．
分析： 由四边形ABCD是平行四边形，即可得BC=AD=4，AB∥CD，继而可证得△FEC∽△FAB，由相似三角形的对应边成比例，即可求得答案．
解答： 解：∵四边形ABCD是平行四边形，
∴BC=AD=4，AB∥CD，
∴△FEC∽△FAB，
∴
==，
∴
=
，
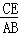∴CF=BC=×4=2．
故答案为：2．
点评： 此题考查了相似三角形的判定与性质以及平行四边形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
发散思维新课堂系列答案
相关题目
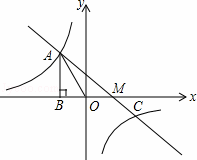
图象过第二象限内的点A（﹣2，m），作AB⊥x轴于点B，Rt△AOB面积为3．
的图象上另一点C（4，﹣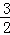
）
+
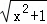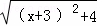的几何意义，并求它的最小值．
+
=
+
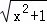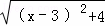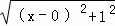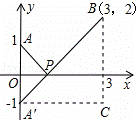
，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则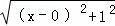
可以看成点P与点A（0，1）的距离，
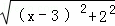可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA+PB的最小值．
PA′+PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C=3，CB=3，所以A′B=3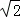
，即原式的最小值为3
+
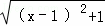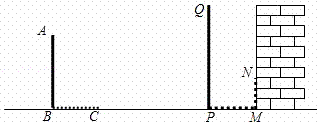
的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B（2，3）或（2，﹣3）的距离之和．（填写点B的坐标）
+
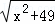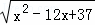的最小值．
