题目内容
如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AE•BC=BD•AC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.

考点: 相似三角形的判定与性质.
分析: (1)由BE平分∠ABC交AC于点E,ED∥BC,可证得BD=DE,△ADE∽△ABC,然后由相似三角形的对应边成比例,证得AE•BC=BD•AC;
(2)根据三角形面积公式与S△ADE=3,S△BDE=2,可得AD:BD=3:2,然后由平行线分线段成比例定理,求得BC的长.
解答: (1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE.…(1分)
∵DE∥BC,
∴∠DEB=∠CBE…(1分)
∴∠ABE=∠DEB.
∴BD=DE,…(1分)
∵DE∥BC,
∴△ADE∽△ABC,
∴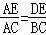 …(1分)
…(1分)
∴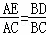 ,
,
∴AE•BC=BD•AC;…(1分)
(2)解:设△ABE中边AB上的高为h.
∴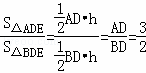 ,…(2分)
,…(2分)
∵DE∥BC,
∴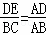 . …(1分)
. …(1分)
∴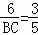 ,
,
∴BC=10. …(2分)
点评: 此题考查了相似三角形的判定与性质、平行线分线段成比例定理以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
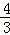 x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.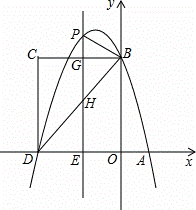
 B.
B. C.
C. D.
D.
 的你告诉他:他的这个想法能实现吗?为什么?
的你告诉他:他的这个想法能实现吗?为什么?