题目内容
2.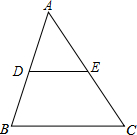 如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.
如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.
分析 根据三角形的中位线得出DE=$\frac{1}{2}$BC,DE∥BC,推出△ADE∽△ABC,再求出△ABC和△ADE的面积比值求出,进而可求出梯形DBCE的面积.
解答 解:∵点D、E分别是AB、AC边的中点,
∴DE是三角形的中位线,
∴DE=$\frac{1}{2}$BC,DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=\frac{1}{4}$,
∵△ABC的面积为12cm2,
∴△ADE的面积为3cm2,
∴梯形DBCE的面积=12-3=9cm2,
故答案为:9.
点评 本题考查了三角形的中位线和相似三角形的性质和判定的应用,解此题的关键是求出△ABC和△ADE的面积比值,题型较好,但是一道比较容易出错的题目.

练习册系列答案
相关题目
8.计算(-2)-5的结果等于( )
| A. | -7 | B. | -3 | C. | 3 | D. | 7 |
13. 如图,四边形ABCD为⊙O的内接四边形,已知∠ADC=130°,则∠AOC的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠ADC=130°,则∠AOC的度数为( )
 如图,四边形ABCD为⊙O的内接四边形,已知∠ADC=130°,则∠AOC的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠ADC=130°,则∠AOC的度数为( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
10.已知甲、乙、丙均为x的一次多项式,且其一次项的系数皆为正整数.若甲与乙相乘为x2-4,乙与丙相乘为x2+15x-34,则甲与丙相加的结果与下列哪一个式子相同?( )
| A. | 2x+19 | B. | 2x-19 | C. | 2x+15 | D. | 2x-15 |
12.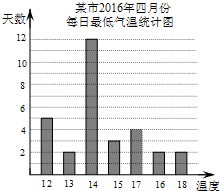 如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )
如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )
 如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )
如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )| A. | 14℃,14℃ | B. | 15℃,15℃ | C. | 14℃,15℃ | D. | 15℃,14℃ |
 如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=2$\sqrt{2}$.
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=2$\sqrt{2}$.
 如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC
如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC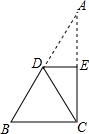 (1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.
(1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.