题目内容
13. 如图,四边形ABCD为⊙O的内接四边形,已知∠ADC=130°,则∠AOC的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠ADC=130°,则∠AOC的度数为( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
分析 先依据内接四边形的性质求得∠B的度数,然后再依据圆周角定理求得∠AOC的度数即可.
解答 解:∵四边形ABCD为⊙O的内接四边形,
∴∠B+∠D=180°,
∴∠B=180°-130°=50°,
∴∠AOC=2∠B=100°.
故选:C.
点评 本题主要考查的是圆内接四边形的性质、圆周角定理的应用,求得∠B的度数是解题的关键.

练习册系列答案
相关题目
19.函数y=$\frac{\sqrt{x}}{x-2}$的自变量x的取值范围是( )
| A. | x≥0且x≠2 | B. | x≥0 | C. | x≠2 | D. | x>2 |
20.若分式$\frac{x-2}{x+3}$的值为0,则x的值是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
8. 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 130° |
18.下列说法不正确的是( )
| A. | 选举中,人们通常最关心的数据是众数 | |
| B. | 从1,2,3,4,5中随机抽取一个数,取得奇数的可能性比较大 | |
| C. | 甲、乙两人在相同条件下各射击10次,他们的平均成绩相同,方差分别为S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 数据3,5,4,1,-2的中位数是4 |
5.如图,AB是半圆O的直径,∠DBA=20°,则∠C的大小是( )

| A. | 70° | B. | 100° | C. | 110° | D. | 140° |
3. 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
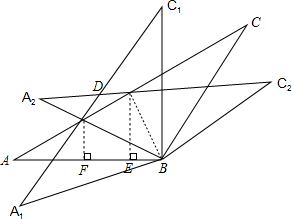 如图,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B旋转30°得到△A1BC1,设AC交A1C1于点D,则点D到AB的距离为$\sqrt{3}$-1或1.
如图,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B旋转30°得到△A1BC1,设AC交A1C1于点D,则点D到AB的距离为$\sqrt{3}$-1或1.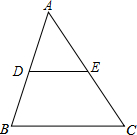 如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.
如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.