题目内容
11. (1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.
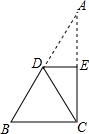
(1)解方程组:$\left\{\begin{array}{l}{x-y=2}\\{x-y=y+1}\end{array}\right.$.(2)如图,Rt△ABC中,∠ACB=90°,将Rt△ABC向下翻折,使点A与点C重合,折痕为DE.求证:DE∥BC.
分析 (1)根据方程组的解法解答即可;
(2)由翻折可知∠AED=∠CED=90°,再利用平行线的判定证明即可.
解答 解:(1)$\left\{\begin{array}{l}{x-y=2①}\\{x-y=y+1②}\end{array}\right.$,
①-②得:y=1,
把y=1代入①可得:x=3,
所以方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$;
(2)∵将Rt△ABC向下翻折,使点A与点C重合,折痕为DE.
∴∠AED=∠CED=90°,
∴∠AED=∠ACB=90°,
∴DE∥BC.
点评 本题考查的是图形的翻折变换,涉及到平行线的判定,熟知折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
19.已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为( )
| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
3. 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
1.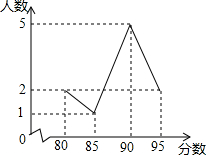 在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
 在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )| A. | 95 | B. | 90 | C. | 85 | D. | 80 |
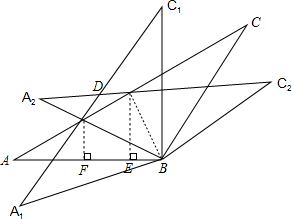 如图,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B旋转30°得到△A1BC1,设AC交A1C1于点D,则点D到AB的距离为$\sqrt{3}$-1或1.
如图,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B旋转30°得到△A1BC1,设AC交A1C1于点D,则点D到AB的距离为$\sqrt{3}$-1或1.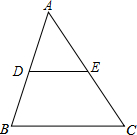 如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.
如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2. 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为$\frac{3\sqrt{3}-π}{2}$.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为$\frac{3\sqrt{3}-π}{2}$. 由六个相同的立方体搭成的几何体如图所示,则它的主视图是( )
由六个相同的立方体搭成的几何体如图所示,则它的主视图是( )