题目内容
7.如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).

分析 (1)根据三角形的外角的性质、结合题意计算即可;
(2)作BD⊥CA交CA的延长线于D,设BD=xm,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.
解答 解:(1)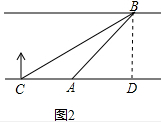 由题意得,∠BAD=45°,∠BCA=30°,
由题意得,∠BAD=45°,∠BCA=30°,
∴∠CBA=∠BAD-∠BCA=15°;
(2)作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD=$\frac{BD}{tan30°}$=$\sqrt{3}$x,
∵∠BAD=45°,
∴AD=BD=x,
则$\sqrt{3}$x-x=60,
解得x=$\frac{60}{\sqrt{3}-1}$≈82,
答:这段河的宽约为82m.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y3<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y2<y1<y3 |
18.下列说法不正确的是( )
| A. | 选举中,人们通常最关心的数据是众数 | |
| B. | 从1,2,3,4,5中随机抽取一个数,取得奇数的可能性比较大 | |
| C. | 甲、乙两人在相同条件下各射击10次,他们的平均成绩相同,方差分别为S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 数据3,5,4,1,-2的中位数是4 |
15.下列立体图形中,主视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为( )
| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
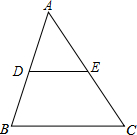 如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.
如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2. 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为$\frac{3\sqrt{3}-π}{2}$.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为$\frac{3\sqrt{3}-π}{2}$.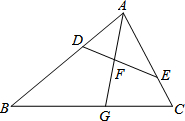 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且$\frac{AD}{AC}=\frac{DF}{CG}$.
如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且$\frac{AD}{AC}=\frac{DF}{CG}$.