题目内容
14. 如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC
如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC(1)线段BC的长等于$\sqrt{2}$;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点A为圆心,以线段BC的长为半径画弧,与射线BA交于点D,使线段OD的长等于$\sqrt{6}$
②连OD,在OD上画出点P,使OP的长等于$\frac{2\sqrt{6}}{3}$,请写出画法,并说明理由.
分析 (1)由圆的半径为1,可得出AB=AC=1,结合勾股定理即可得出结论;
(2)①结合勾股定理求出AD的长度,从而找出点D的位置,根据画图的步骤,完成图形即可;
②根据线段的三等分点的画法,结合OA=2AC,即可得出结论.
解答 解:(1)在Rt△BAC中,AB=AC=1,∠BAC=90°,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
(2)①在Rt△OAD中,OA=2,OD=$\sqrt{6}$,∠OAD=90°,
∴AD=$\sqrt{O{D}^{2}-O{A}^{2}}$=$\sqrt{2}$=BC.
∴以点A为圆心,以线段BC的长为半径画弧,与射线BA交于点D,使线段OD的长等于$\sqrt{6}$.
依此画出图形,如图1所示.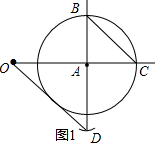
故答案为:A;BC.
②∵OD=$\sqrt{6}$,OP=$\frac{2\sqrt{6}}{3}$,OC=OA+AC=3,OA=2,
∴$\frac{OA}{OC}=\frac{OP}{OD}=\frac{2}{3}$.
故作法如下:
连接CD,过点A作AP∥CD交OD于点P,P点即是所要找的点.
依此画出图形,如图2所示.
点评 本题考查了作图中的寻找线段的三等分点以及勾股定理,解题的关键是:(1)利用勾股定理求出BC的长;(2)①利用勾股定理求出AD的长;②会画线段的三等分点.本题属于中档题,难度不大,(2)中巧妙的借助了OA=2AC,从而利用比例找出了点P的位置.

练习册系列答案
相关题目
20.若分式$\frac{x-2}{x+3}$的值为0,则x的值是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
5.如图,AB是半圆O的直径,∠DBA=20°,则∠C的大小是( )

| A. | 70° | B. | 100° | C. | 110° | D. | 140° |
19.已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为( )
| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
3. 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
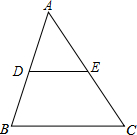 如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.
如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.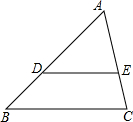 如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若△ADE与△ABC的周长之比为2:3,AD=4,则DB=2.
如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若△ADE与△ABC的周长之比为2:3,AD=4,则DB=2. 为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:
为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题: