题目内容
9．
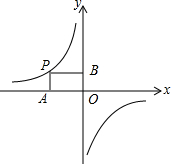如图，点P在反比例函数y=$\frac{k}{x}$（k≠0）的图象上，过点P分别作PA⊥x轴于点A，PB⊥y轴于点B，若四边形PAOB的面积为12，则k的值为（ ）| A． | 24 | B． | 12 | C． | -24 | D． | -12 |
分析 根据反比例函数k的几何意义可得|k|=4，再根据图象在二、四象限可确定k＜0，进而得到解析式．
解答 解：∵S矩形PAOB=12，
∴|k|=12，
∵图象在二、四象限，
∴k＜0，
∴k=-12，
故选D．
点评 本题考查反比例函数系数k的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|．本知识点是中考的重要考点，同学们应高度关注．
练习册系列答案
字词句段篇系列答案
相关题目
19．
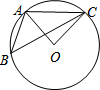如图，点A、B、C均在⊙O上，若∠ABC=40°，则∠AOC的大小是（ ）
如图，点A、B、C均在⊙O上，若∠ABC=40°，则∠AOC的大小是（ ）| A． | 90° | B． | 80° | C． | 70° | D． | 50° |
17．下列各式从左到右的变形正确的是（ ）
| A． | $\frac{b}{a}=\frac{bc}{ac}$ | B． | $\frac{b}{a}=\frac{b+c}{a+c}$ | C． | $\frac{b}{a}=\frac{b^2}{a^2}$ | D． | $\frac{b}{a}=\frac{ab}{a^2}$ |
如图，在⊙O中．弦AB，CD相交于点E，若AE=BE=3，CE=2，则CD的值为$\frac{13}{2}$．
14．
如图，已知A、B、C为⊙O上三点，连接BC、AC、OA、OB，若∠ACB=50°，OA=3，则扇形AOB的面积为（ ）
如图，已知A、B、C为⊙O上三点，连接BC、AC、OA、OB，若∠ACB=50°，OA=3，则扇形AOB的面积为（ ）| A． | $\frac{5π}{4}$ | B． | $\frac{5π}{2}$ | C． | 5π | D． | 10π |
1．在Rt△ACB中，∠C=90°，AC=1，BC=2，则sinB的值为（ ）
| A． | $\frac{{2\sqrt{5}}}{5}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{1}{2}$ |
18．
如图，等边三角形ABC内接于⊙O，若AB=3，则图中阴影部分的面积为（ ）
如图，等边三角形ABC内接于⊙O，若AB=3，则图中阴影部分的面积为（ ）| A． | $\frac{3π}{2}-\frac{9}{4}\sqrt{3}$ | B． | $\frac{3π}{2}-\frac{9}{2}\sqrt{3}$ | C． | $π-\frac{3}{4}\sqrt{3}$ | D． | $π-\frac{3}{2}\sqrt{3}$ |
19．下列各式中，计算正确的是（ ）
| A． | （a-4）（a+4）=a2-4 | B． | （4y+1）（4y-1）=16y2-1 | C． | （2x-3）（x+3）=2x2-9 | D． | （x+2）（x+2）=x2+4 |