题目内容
14．
如图，已知A、B、C为⊙O上三点，连接BC、AC、OA、OB，若∠ACB=50°，OA=3，则扇形AOB的面积为（ ）| A． | $\frac{5π}{4}$ | B． | $\frac{5π}{2}$ | C． | 5π | D． | 10π |
分析 根据圆周角定理求出∠AOB，代入扇形的面积公式运算即可．
解答 解：∵∠ACB=50°，
∴∠AOB=2∠ACB=100°，
∴扇形AOB的面积=$\frac{100•π×{3}^{3}}{360}$=$\frac{5π}{2}$，
故选B．
点评 本题考查了扇形的面积计算及圆周角定理的知识，属于基础题，注意熟练掌握扇形的面积公式．
练习册系列答案
相关题目
如图，O为坐标原点，⊙O的半径为1，点P是直线y=-2x-6上的动点，过点P作⊙O的切线PA、PB，A、B为切点，连接OA、OB，则四边形OAPB的面积的最小值为$\frac{\sqrt{155}}{5}$．
2．
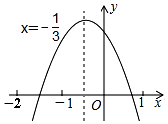如图是二次函数y=ax2+bx+c（a≠0）的图象，有下列结论：①ab＞0；②a+b+c＜0；③b+2c＜0；④a-2b+4c＞0；⑤a=$\frac{3}{2}$b．其中正确的有（ ）
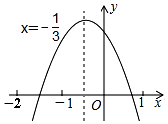如图是二次函数y=ax2+bx+c（a≠0）的图象，有下列结论：①ab＞0；②a+b+c＜0；③b+2c＜0；④a-2b+4c＞0；⑤a=$\frac{3}{2}$b．其中正确的有（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
9．
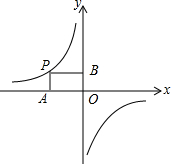如图，点P在反比例函数y=$\frac{k}{x}$（k≠0）的图象上，过点P分别作PA⊥x轴于点A，PB⊥y轴于点B，若四边形PAOB的面积为12，则k的值为（ ）
如图，点P在反比例函数y=$\frac{k}{x}$（k≠0）的图象上，过点P分别作PA⊥x轴于点A，PB⊥y轴于点B，若四边形PAOB的面积为12，则k的值为（ ）| A． | 24 | B． | 12 | C． | -24 | D． | -12 |
19．以下选项是二次函数f（x）=x2+（m-3）x+1的图象与x轴的交点（x1，0）（x2，0）均在A（1，0）右侧的充要条件的是（ ）
| A． | $\left\{\begin{array}{l}f（1）＞0\\ \frac{3-m}{2}＞1\\△≥0\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x_1}+{x_2}＞2\\{x_1}{x_2}＞1\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}f（1）＞0\\ \frac{3-m}{2}＞2\\△＞0\end{array}\right.$ | D． | $\left\{\begin{array}{l}f（1）＜0\\△＞0\end{array}\right.$ |
6．函数y=$\frac{1}{x}$中自变量x的取值范围是（ ）
| A． | x≠1 | B． | x≠0 | C． | x＞0 | D． | 全体实数 |
