题目内容
18. 如图,等边三角形ABC内接于⊙O,若AB=3,则图中阴影部分的面积为( )
如图,等边三角形ABC内接于⊙O,若AB=3,则图中阴影部分的面积为( )| A. | $\frac{3π}{2}-\frac{9}{4}\sqrt{3}$ | B. | $\frac{3π}{2}-\frac{9}{2}\sqrt{3}$ | C. | $π-\frac{3}{4}\sqrt{3}$ | D. | $π-\frac{3}{2}\sqrt{3}$ |
分析 连接OB、OC,过O作OD⊥BC于D,根据垂径定理求出BD,根据等边三角形性质求出∠OBC,根据勾股定理得到OB,分别求出扇形BOC和三角形OBC的面积,即可得出答案.
解答 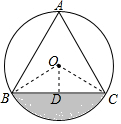 解:连接OB、OC,过O作OD⊥BC于D,
解:连接OB、OC,过O作OD⊥BC于D,
则BD=DC=$\frac{3}{2}$,∠ODB=90°,
∵三角形ABC是等边三角形,
∴∠ABC=60°,
∴∠OBC=30°,∠BOD=90°-30°=60°,
∴OD=$\frac{\sqrt{3}}{3}$DB=$\frac{\sqrt{3}}{2}$cm,∠BOC=60°+60°=120°,
由勾股定理得:BO=$\sqrt{(\frac{3}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{3}$,
∴阴影部分的面积S=S扇形BOC-S△OBC=$\frac{120•π×(\sqrt{3})^{2}}{360}$-$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$=π-$\frac{3}{4}$$\sqrt{3}$,
故选C.
点评 本题考查了扇形面积公式,等边三角形的性质,三角形的外接圆,三角形面积,含30度角的直角三角形性质的应用,注意:圆心角为n°,半径为r的扇形的面积为S=$\frac{nπ{r}^{2}}{360}$.

练习册系列答案
相关题目
8.下列算式中,运算结果为负数的是( )
| A. | -(-3) | B. | |-3| | C. | (-3)2 | D. | (-3)3 |
9.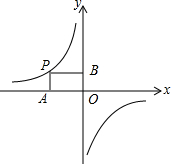 如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
 如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )| A. | 24 | B. | 12 | C. | -24 | D. | -12 |
6.函数y=$\frac{1}{x}$中自变量x的取值范围是( )
| A. | x≠1 | B. | x≠0 | C. | x>0 | D. | 全体实数 |
10.如图,在边长为a的正方形的右下角,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个平行四边形,这一过程可以验证一个关于a,b的等式为( )
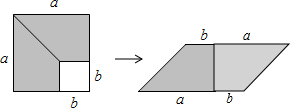

| A. | (a-b)2=a2-2ab+b2 | B. | a2+ab=a(a+b) | C. | (a+b)2=a2+2ab+b2 | D. | a2-b2=(a+b)(a-b) |
7.下列各数中,最大的数是( )
| A. | 1 | B. | -2 | C. | |-3| | D. | 0 |
8. 如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD的长为( )
如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD的长为( )
 如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD的长为( )
如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
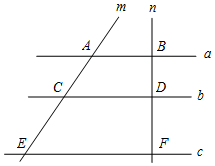 如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,AE=10,BD=3,则DF的值是( )
如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,AE=10,BD=3,则DF的值是( )